题目内容
 如图,直线AB、CD相交于点O,OE平分∠BOD,AOD-∠DOB=72°.求∠AOC和∠DOE的度数.
如图,直线AB、CD相交于点O,OE平分∠BOD,AOD-∠DOB=72°.求∠AOC和∠DOE的度数.考点:对顶角、邻补角,角平分线的定义
专题:
分析:根据邻补角的性质,可得∠AOD与∠BOD的关系,根据解二元一次方程组,可得∠BOD,根据对顶角的性质,可得∠∠AOC的度数,根据角平分线的性质,可得∠∠DOE的数.
解答:解:由邻补角的性质,得
∠AOD+∠BOD=180°,
,
解得
.
由对顶角相等,得
∠AOC=∠BOD=54°,
由OE平分∠BOD,得
∠DOE=
∠DOB=27°.
∠AOD+∠BOD=180°,
|
解得
|
由对顶角相等,得
∠AOC=∠BOD=54°,
由OE平分∠BOD,得
∠DOE=
| 1 |
| 2 |
点评:本题考查了对顶角、邻补角,利用了邻补角的互补,对顶角相等.

练习册系列答案
相关题目
已知圆柱的母线长5,侧面积为30π,则圆柱的底面直径长是( )
| A、3 | B、6 | C、9 | D、12 |
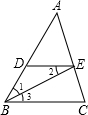 请把下列说理过程补充完整:
请把下列说理过程补充完整:?已知:如图,DE∥BC,BE平分∠ABC.你能说明∠1=∠3吗?
理由:∵BE平分∠ABC(已知),
∴∠1=
又∵DE∥BC(已知),
∴∠2=
∴∠1=∠3(等量代换).
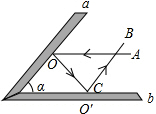 如图,两个平面镜a、b的夹角为α,平行于b的光线AO入射到α上,经过两次反射后的反射光线0’B平行于a,则角α等于( )
如图,两个平面镜a、b的夹角为α,平行于b的光线AO入射到α上,经过两次反射后的反射光线0’B平行于a,则角α等于( )| A、70° | B、60° |
| C、45° | D、30° |
 如图,正方形ABCD的边长为4,点M,N,P分别为AD,BC,CD的中点.现从点P观察线段AB,当长度为1的线段l(图中的黑粗线)以每秒1个单位长的速度沿线段MN从左向右运动时,l将阻挡部分观察视线,在△PAB区域内形成盲区.设l的左端点从M点开始,运动时间为t秒(0≤t≤3).设△PAB区域内的盲区面积为y(平方单位).
如图,正方形ABCD的边长为4,点M,N,P分别为AD,BC,CD的中点.现从点P观察线段AB,当长度为1的线段l(图中的黑粗线)以每秒1个单位长的速度沿线段MN从左向右运动时,l将阻挡部分观察视线,在△PAB区域内形成盲区.设l的左端点从M点开始,运动时间为t秒(0≤t≤3).设△PAB区域内的盲区面积为y(平方单位).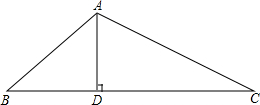 如图,在△ABC中,AD⊥BC于D,已知AD=9,tan∠ABD=
如图,在△ABC中,AD⊥BC于D,已知AD=9,tan∠ABD=