题目内容
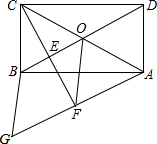 如图,在矩形ABCD中,AC、BD相交于点O,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BO,连接BG、DF.若AG=13,CF=6,求四边形BOFG的周长.
如图,在矩形ABCD中,AC、BD相交于点O,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BO,连接BG、DF.若AG=13,CF=6,求四边形BOFG的周长.考点:菱形的判定与性质,矩形的性质
专题:
分析:根据一组对边平行且相等的四边形是平行四边形判断出四边形BGFO是平行四边形,根据直角三角形斜边上的中线等于斜边的一半可得OF=
AC,然后求出OB=OF,判断出四边形BOFG是菱形,设GF=x,表示出AF、AC,然后利用勾股定理列出方程求出x,再根据菱形的周长公式列式计算即可得解.
| 1 |
| 2 |
解答:解:∵AF∥BD,FG=BO,
∴四边形BGFO是平行四边形,
∵四边形ABCD是矩形,
∴OA=OB=OC=
AC,
∵CE⊥BD,AF∥BD,
∴CF⊥AF,
∴OF=
AC,
∴OB=OF,
∴四边形BOFG是菱形,
设GF=x,则AF=13-x,AC=2OF=2x,
在Rt△ACF中,由勾股定理得,AF2+CF2=AC2,
即(13-x)2+62=(2x)2,
整理得,3x2+26x-205=0,
解得x1=5,x2=-
(舍去),
∴GF=5,
四边形BOFG的周长=4×5=20.
∴四边形BGFO是平行四边形,
∵四边形ABCD是矩形,
∴OA=OB=OC=
| 1 |
| 2 |
∵CE⊥BD,AF∥BD,
∴CF⊥AF,
∴OF=
| 1 |
| 2 |
∴OB=OF,
∴四边形BOFG是菱形,
设GF=x,则AF=13-x,AC=2OF=2x,
在Rt△ACF中,由勾股定理得,AF2+CF2=AC2,
即(13-x)2+62=(2x)2,
整理得,3x2+26x-205=0,
解得x1=5,x2=-
| 41 |
| 3 |
∴GF=5,
四边形BOFG的周长=4×5=20.
点评:本题考查了菱形的判定与性质,矩形的性质,直角三角形斜边上的中线等于斜边的一半的性质,熟记各性质并利用勾股定理列出方程是解题的关键.

练习册系列答案
相关题目
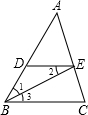 请把下列说理过程补充完整:
请把下列说理过程补充完整:?已知:如图,DE∥BC,BE平分∠ABC.你能说明∠1=∠3吗?
理由:∵BE平分∠ABC(已知),
∴∠1=
又∵DE∥BC(已知),
∴∠2=
∴∠1=∠3(等量代换).
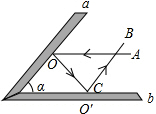 如图,两个平面镜a、b的夹角为α,平行于b的光线AO入射到α上,经过两次反射后的反射光线0’B平行于a,则角α等于( )
如图,两个平面镜a、b的夹角为α,平行于b的光线AO入射到α上,经过两次反射后的反射光线0’B平行于a,则角α等于( )| A、70° | B、60° |
| C、45° | D、30° |
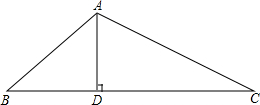 如图,在△ABC中,AD⊥BC于D,已知AD=9,tan∠ABD=
如图,在△ABC中,AD⊥BC于D,已知AD=9,tan∠ABD= 如图,长方形ABCD沿AE折叠,使点B落在CD边上的点F处,如果∠EFC=60°,那么∠BAE等于多少度?请说明理由.
如图,长方形ABCD沿AE折叠,使点B落在CD边上的点F处,如果∠EFC=60°,那么∠BAE等于多少度?请说明理由.