题目内容
 如图,△ABC中,D、E分别是AB和AC的中点.△ABC的周长为8,则△ADE的周长是
如图,△ABC中,D、E分别是AB和AC的中点.△ABC的周长为8,则△ADE的周长是考点:三角形中位线定理
专题:
分析:根据三角形的中位线定理可以证得DE∥BC,则△ADE∽△ABC,根据相似三角形的性质即可求解.
解答:解:∵D、E分别是AB和AC的中点,
∴DE∥BC,且DE=
BC,即
=
,
∴△ADE∽△ABC,
∴
=
,
∴△ADE的周长是:
×8=4.
故答案是:4.
∴DE∥BC,且DE=
| 1 |
| 2 |
| DE |
| BC |
| 1 |
| 2 |
∴△ADE∽△ABC,
∴
| C△ADE |
| C△ABC |
| 1 |
| 2 |
∴△ADE的周长是:
| 1 |
| 2 |
故答案是:4.
点评:本题考查了三角形中位线定理以及相似三角形的性质定理,理解定理是关键.

练习册系列答案
相关题目
 如图,直线a、b被直线c所截,∠1=∠3,直线a与直线b平行吗?为什么?
如图,直线a、b被直线c所截,∠1=∠3,直线a与直线b平行吗?为什么? 如图,一个长方形的饮料盒,它的长、宽、高分别上4厘米、3厘米、12厘米.吸管要露出4厘米,那么吸管最多应该有多长?
如图,一个长方形的饮料盒,它的长、宽、高分别上4厘米、3厘米、12厘米.吸管要露出4厘米,那么吸管最多应该有多长? 四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,AB=4cm,求EF的长.
四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,AB=4cm,求EF的长.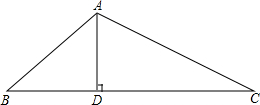 如图,在△ABC中,AD⊥BC于D,已知AD=9,tan∠ABD=
如图,在△ABC中,AD⊥BC于D,已知AD=9,tan∠ABD=