题目内容
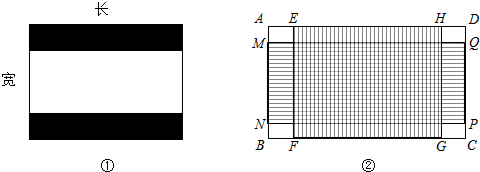
 张师傅在铺地板时发现,用8块大小一样的小长方形瓷砖恰好可以拼成一个大的长方形,如图(1),然后,他用这8块瓷砖又拼出一个正方形,如图(2),中间恰好空出一个边长为10cm的小正方形(阴影部分),假设小长方形的长为y,宽为x,且y>x,
张师傅在铺地板时发现,用8块大小一样的小长方形瓷砖恰好可以拼成一个大的长方形,如图(1),然后,他用这8块瓷砖又拼出一个正方形,如图(2),中间恰好空出一个边长为10cm的小正方形(阴影部分),假设小长方形的长为y,宽为x,且y>x,(1)写出图(1)中y与x的函数关系式;
(2)写出图中(2)y与x的函数关系式;
(3)求出每块瓷砖的长与宽.
考点:一次函数的应用,二元一次方程组的应用
专题:
分析:(1)观察图形,三个长方形的长的和正好等于其余的长方形的宽的和,然后列式整理即可;
(2)观察图形,两个长方形的宽的和比长方形的长多中间小正方形的边长,然后列式整理即可;
(3)联立组成方程组,然后求解即可.
(2)观察图形,两个长方形的宽的和比长方形的长多中间小正方形的边长,然后列式整理即可;
(3)联立组成方程组,然后求解即可.
解答:解:(1)由图1可知,3y=5x,
所以,y=
x;
(2)由图2可知,2x-y=10,
所以,y=2x-10;
(3)联立
,
解得
.
答:每块瓷砖的长与宽分别为50cm,30cm.
所以,y=
| 5 |
| 3 |
(2)由图2可知,2x-y=10,
所以,y=2x-10;
(3)联立
|
解得
|
答:每块瓷砖的长与宽分别为50cm,30cm.
点评:本题考查了一次函数的应用,二元一次方程组的应用,仔细观察图形,由拼接成的长方形和正方形得到x、y的关系式是解题的关键.

练习册系列答案
相关题目
已知圆柱的母线长5,侧面积为30π,则圆柱的底面直径长是( )
| A、3 | B、6 | C、9 | D、12 |
 如图,⊙O直径AB=8,∠CBD=30°,则CD=( )
如图,⊙O直径AB=8,∠CBD=30°,则CD=( )| A、4 | ||
| B、6 | ||
| C、3 | ||
D、2
|
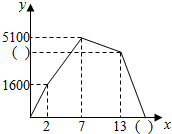 甲骑自行车,乙步行均从A地出发,以各自的速度匀速向B地行驶,其中甲先出发到达B地,停留6分钟后,按原路原速返回到A地,乙则一直步行到B地,如图是甲乙两人之间的距离y米与甲用时x之间的部分函数图象.
甲骑自行车,乙步行均从A地出发,以各自的速度匀速向B地行驶,其中甲先出发到达B地,停留6分钟后,按原路原速返回到A地,乙则一直步行到B地,如图是甲乙两人之间的距离y米与甲用时x之间的部分函数图象.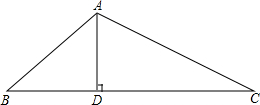 如图,在△ABC中,AD⊥BC于D,已知AD=9,tan∠ABD=
如图,在△ABC中,AD⊥BC于D,已知AD=9,tan∠ABD=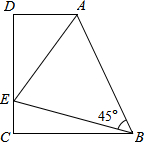 如图,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=12,∠ABE=45°,若AE=10.求CE的长度.
如图,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=12,∠ABE=45°,若AE=10.求CE的长度.