题目内容
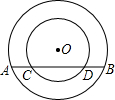已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C，D（如图）．（1）求证：AC=BD；
（2）若大圆的半径R=10，小圆的半径r=8，且圆O到直线AB的距离为6，求AC的长．
考点：垂径定理,勾股定理
专题：几何综合题
分析：（1）过O作OE⊥AB，根据垂径定理得到AE=BE，CE=DE，从而得到AC=BD；
（2）由（1）可知，OE⊥AB且OE⊥CD，连接OC，OA，再根据勾股定理求出CE及AE的长，根据AC=AE-CE即可得出结论．
（2）由（1）可知，OE⊥AB且OE⊥CD，连接OC，OA，再根据勾股定理求出CE及AE的长，根据AC=AE-CE即可得出结论．
解答：
（1）证明：过O作OE⊥AB于点E，
则CE=DE，AE=BE，
∴BE-DE=AE-CE，即AC=BD；
（2）解：由（1）可知，OE⊥AB且OE⊥CD，连接OC，OA，
∴OE=6，
∴CE=
=
=2
，AE=
=
=8，
∴AC=AE-CE=8-2
．
（1）证明：过O作OE⊥AB于点E，则CE=DE，AE=BE，
∴BE-DE=AE-CE，即AC=BD；
（2）解：由（1）可知，OE⊥AB且OE⊥CD，连接OC，OA，
∴OE=6，
∴CE=
| OC2-OE2 |
| 82-62 |
| 7 |
| OA2-OE2 |
| 102-62 |
∴AC=AE-CE=8-2
| 7 |
点评：本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
如图，边长为n的正方形OABC的边OA，OC在坐标轴上，点A1，A2，…，An-1为OA的n等分点，点B1，B2，…，Bn-1为CB的n等分点，连结A1B1，A2B2，…，An-1Bn-1，分别交曲线y=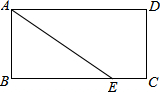
如图，在矩形ABCD中，AB=2，AD=4，点E是BC边上的一点，连接AE，若CE=1，求AE的长．
已知：关于x的一元二次方程mx2+（m-3）x-3=0．
如图，AB是⊙O的直径，OD垂直于弦AC于点E，且交⊙O于点D，F是BA延长线上一点，若∠CDB=∠BFD．