题目内容
 已知:关于x的一元二次方程mx2+(m-3)x-3=0.
已知:关于x的一元二次方程mx2+(m-3)x-3=0.(1)求证:无论m取何值,此方程总有两个实数根;
(2)设抛物线y=mx2+(m-3)x-3,证明:此函数图象一定过x轴,y轴上的两个定点(设x轴上的定点为点A,y轴上的定点为点C);
(3)设此函数的图象与x轴的另一交点为B,当△ABC为锐角三角形时,求m的取值范围.
考点:二次函数综合题
专题:综合题
分析:(1)证明方程判别式为非负数即可;
(2)求出mx2+(m-3)x-3=0的两个根,可得x轴上的定点,根据解析式可确定y轴定点为(0,3);
(3)先确定A、B、C三点坐标,求出当∠ACB是直角时,点B的坐标,依次为临界,确定△ABC为锐角三角形时,求m的取值范围.
(2)求出mx2+(m-3)x-3=0的两个根,可得x轴上的定点,根据解析式可确定y轴定点为(0,3);
(3)先确定A、B、C三点坐标,求出当∠ACB是直角时,点B的坐标,依次为临界,确定△ABC为锐角三角形时,求m的取值范围.
解答:解:(1)△=(m-3)2+12m=(m+3)2
∵(m+3)2≥0
∴无论m取何值,此方程总有两个实数根.
(2)由公式法:x1,2=
=
∴x1=-1,x2=
,
∴此函数图象一定过x轴,y轴上的两个定点,分别为A(-1,0),C(0,-3).
 (3)由(2)可知抛物线开口向上,且过点A(-1,0),C(0,-3)和B(
(3)由(2)可知抛物线开口向上,且过点A(-1,0),C(0,-3)和B(
,0).
观察图象,当m<0时,△ABC为钝角三角形,不符合题意.
当m>0时,可知若∠ACB=90°时,
可证△AOC∽△COB.
∴
=
.
∴|OC|2=|OA|•|OB|.
∴32=1×|OB|.
∴OB=9.即B(9,0).
∴当0<
<9时,△ABC为锐角三角形.
即当m>
时,△ABC为锐角三角形.
∵(m+3)2≥0
∴无论m取何值,此方程总有两个实数根.
(2)由公式法:x1,2=
3-m±
| ||
| 2m |
| 3-m±(m+3) |
| 2m |
∴x1=-1,x2=
| 3 |
| m |
∴此函数图象一定过x轴,y轴上的两个定点,分别为A(-1,0),C(0,-3).
 (3)由(2)可知抛物线开口向上,且过点A(-1,0),C(0,-3)和B(
(3)由(2)可知抛物线开口向上,且过点A(-1,0),C(0,-3)和B(| 3 |
| m |
观察图象,当m<0时,△ABC为钝角三角形,不符合题意.
当m>0时,可知若∠ACB=90°时,
可证△AOC∽△COB.
∴
| AO |
| CO |
| CO |
| BO |
∴|OC|2=|OA|•|OB|.
∴32=1×|OB|.
∴OB=9.即B(9,0).
∴当0<
| 3 |
| m |
即当m>
| 1 |
| 3 |
点评:本题考查了二次函数的综合,涉及了根的判别式、相似三角形的判定与性质,解答本题的关键是分类讨论思想及数形结合思想的运用,难度较大.

练习册系列答案
相关题目
 已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(-1,0),对称轴为直线x﹦-2,点C是抛物线与y轴的交点,点D是抛物线上另一点,已知以OC为一边的矩形OCDE的面积为8.
已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(-1,0),对称轴为直线x﹦-2,点C是抛物线与y轴的交点,点D是抛物线上另一点,已知以OC为一边的矩形OCDE的面积为8.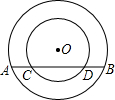 已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图). 如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,设点C的坐标为(0,m)且m<6,△ABC的面积为S,试问:
如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,设点C的坐标为(0,m)且m<6,△ABC的面积为S,试问:
 如图,有两个正方形和一个等边三角形,则图中度数为30°的角有
如图,有两个正方形和一个等边三角形,则图中度数为30°的角有