题目内容
 如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD.
如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD.(1)求证:FD是⊙O的一条切线;
(2)若AB=10,AC=8,求DF的长.
考点:切线的判定,垂径定理,相似三角形的判定与性质
专题:几何图形问题
分析:(1)利用圆周角定理以及平行线的判定得出∠FDO=90°,进而得出答案;
(2)利用垂径定理得出AE的长,再利用相似三角形的判定与性质得出FD的长.
(2)利用垂径定理得出AE的长,再利用相似三角形的判定与性质得出FD的长.
解答:(1)证明:∵∠CDB=∠CAB,∠CDB=∠BFD,
∴∠CAB=∠BFD,
∴FD∥AC(同位角相等,两直线平行),
∵∠AEO=90°,
∴∠FDO=90°,
∴FD是⊙O的一条切线;
(2)解:∵AB=10,AC=8,DO⊥AC,
∴AE=EC=4,AO=5,
∴EO=3,
∵AE∥FD,
∴△AEO∽△FDO,
∴
=
,
∴
=
,
解得:FD=
.
∴∠CAB=∠BFD,
∴FD∥AC(同位角相等,两直线平行),
∵∠AEO=90°,
∴∠FDO=90°,
∴FD是⊙O的一条切线;
(2)解:∵AB=10,AC=8,DO⊥AC,
∴AE=EC=4,AO=5,
∴EO=3,
∵AE∥FD,
∴△AEO∽△FDO,
∴
| AE |
| FD |
| EO |
| DO |
∴
| 3 |
| 5 |
| 4 |
| FD |
解得:FD=
| 20 |
| 3 |
点评:此题主要考查了相似三角形的判定与性质以及切线的判定等知识,得出△AEO∽△FDO是解题关键.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
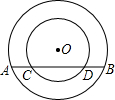 已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图). 如图,一次函数y1=kx+b的图象与反比例函数y2=
如图,一次函数y1=kx+b的图象与反比例函数y2=