题目内容
 如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点,连结A1B1,A2B2,…,An-1Bn-1,分别交曲线y=
如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点,连结A1B1,A2B2,…,An-1Bn-1,分别交曲线y=| n-2 |
| x |
考点:反比例函数图象上点的坐标特征
专题:规律型
分析:先根据正方形OABC的边长为n,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点可知OA15=n,A15B15=15,再根据C15B15=16C15A15表示出C15的坐标,代入反比例函数的解析式求出n的值.
解答:解:∵正方形OABC的边长为n,点A1,A2,…,An-1为OA的n等分点,点B1,B2,…,Bn-1为CB的n等分点,∴OA15=15,A15B15=n,
∵C15B15=16C15A15,
∴C15(15,
),
∵点C15在曲线y=
(x>0)上,
∴15×
=n-2,解得n=17.
故答案为:17.
∵C15B15=16C15A15,
∴C15(15,
| n |
| 17 |
∵点C15在曲线y=
| n-2 |
| x |
∴15×
| n |
| 17 |
故答案为:17.
点评:本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上k=xy为定值是解答此题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
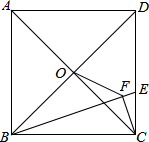 如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为
如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为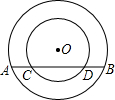 已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).