题目内容
14.在一个纸箱中,装有红色、黄色、绿色的塑料球共60个这些小球除颜色外其他都完全相同,将球充分摇匀后,从中随机摸出一个球,记下它的颜色后再放回箱中,不断重复这一过程,小明发现其中摸到红色球、绿色球的频率分别稳定在15%和45%,则这个纸箱中黄色球的个数可能有24个.分析 在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,设未知数列出方程求解.
解答 解:∵共60个球,其中摸到红色球、绿色球的频率分别稳定在15%和45%,
∴黄球所占的比例为100%-15%-45%=40%,
设盒子中共有黄球x个,则$\frac{x}{60}×100%=40%$,
解得:x=24.
故答案为:24.
点评 本题考查利用频率估计概率.大量反复试验下频率稳定值即概率.关键是根据白球的频率得到相应的等量关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.如果把分式$\frac{2n}{m-n}$中的m和n都扩大2倍,那么分式的值( )
| A. | 不变 | B. | 扩大2倍 | C. | 缩小2倍 | D. | 扩大4倍 |
2. 为了解中学生对我国汉子的掌握情况,某校组织了“汉字知识大赛”活动,随机调查了部分参赛同学的成绩,整理并制作图表如下:
为了解中学生对我国汉子的掌握情况,某校组织了“汉字知识大赛”活动,随机调查了部分参赛同学的成绩,整理并制作图表如下:
(1)表中m=0.2;n=80;本次比赛成绩的中位数落在分数段70≤x<80中;
(2)补全条形统计图;
(3)如果比赛成绩80分以上(含80分)为优秀,全校参加比赛的800名同学中,优秀人数大约有多少人?
 为了解中学生对我国汉子的掌握情况,某校组织了“汉字知识大赛”活动,随机调查了部分参赛同学的成绩,整理并制作图表如下:
为了解中学生对我国汉子的掌握情况,某校组织了“汉字知识大赛”活动,随机调查了部分参赛同学的成绩,整理并制作图表如下:| 分 数 段 | 频数 | 频率 |
| 90≤x<100 | 20 | 0.1 |
| 80≤x<90 | 40 | m |
| 70≤x<80 | n | 0.4 |
| 60≤x<70 | 60 | 0.3 |
(2)补全条形统计图;
(3)如果比赛成绩80分以上(含80分)为优秀,全校参加比赛的800名同学中,优秀人数大约有多少人?
9. 如图,四边形ABCD是⊙O的内接四边形,若∠C=140°,则∠BOD的度数为( )
如图,四边形ABCD是⊙O的内接四边形,若∠C=140°,则∠BOD的度数为( )
 如图,四边形ABCD是⊙O的内接四边形,若∠C=140°,则∠BOD的度数为( )
如图,四边形ABCD是⊙O的内接四边形,若∠C=140°,则∠BOD的度数为( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
6.若点P(1-m,m)在第二象限,则下列关系式正确的是( )
| A. | 0<m<1 | B. | m>0 | C. | m>1 | D. | m<0 |
3.因式分解x2-4的结果是( )
| A. | x(x-4) | B. | x(x-2)2 | C. | (x-2)(x+2) | D. | x(x+2)2 |
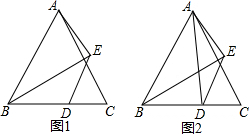 如图,△ABC为等边三角形,点E在∠ABC的平分线上,点D在BC边上,连接AE、DE,且∠AED=120°.
如图,△ABC为等边三角形,点E在∠ABC的平分线上,点D在BC边上,连接AE、DE,且∠AED=120°.