题目内容
18.已知$\sqrt{a-\sqrt{5}-2}$+$\sqrt{b-\sqrt{5}+2}$=0,求$\sqrt{{a}^{2}+{b}^{2}+7}$的值.分析 因为一个数的算术平方根是非负数,先由非负数的和等于0,求出a、b的值,把a、b代入并求出$\sqrt{{a}^{2}+{b}^{2}+7}$的值.
解答 解:∵$\sqrt{a-\sqrt{5}-2}$≥0,$\sqrt{b-\sqrt{5}+2}$≥0,
又∵$\sqrt{a-\sqrt{5}-2}$+$\sqrt{b-\sqrt{5}+2}$=0,
∴a-$\sqrt{5}-2=0$,b-$\sqrt{5}$+2=0,
即a=$\sqrt{5}+2$,b=$\sqrt{5}$-2
∴a2+b2+7=($\sqrt{5}+2$)2+($\sqrt{5}$-2)2+7
=5+4$\sqrt{5}$+4+5-4$\sqrt{5}$+4+7
=25
∴$\sqrt{{a}^{2}+{b}^{2}+7}$
=$\sqrt{25}$
=5.
点评 本题考查了非负数的算式平方根和二次根式的化简.解决本题的关键是根据非负数的和为零求出a、b的值.初中阶段学过的非负数有:一个数的绝对值、一个数的偶次方、一个数的算术平方根.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
6. 如图,已知AB∥CD,BC平分∠ABE,∠C=29°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=29°,则∠BED的度数是( )
 如图,已知AB∥CD,BC平分∠ABE,∠C=29°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=29°,则∠BED的度数是( )| A. | 18° | B. | 29° | C. | 58° | D. | 38° |
13.已知圆锥的底面半径为3cm,母线长为5cm,则圆锥的侧面积是( )
| A. | 20 cm2 | B. | 20π cm2 | C. | 15 cm2 | D. | 15π cm2 |
10.若最简二次根式$\sqrt{1+2a}$与2$\sqrt{3}$是同类二次根式,则a的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | $\frac{5}{2}$ |
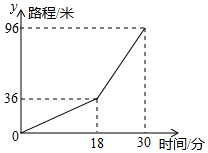 小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.
小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.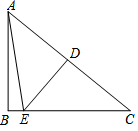 如图,在Rt△ABC中,∠B为直角,DE是AC的垂直平分线,DE交AC于点D,交BC于点E,且∠BAE:∠BAC=1:5,则∠C=40°.
如图,在Rt△ABC中,∠B为直角,DE是AC的垂直平分线,DE交AC于点D,交BC于点E,且∠BAE:∠BAC=1:5,则∠C=40°.