题目内容
7.已知:在Rt△ABC中,∠C=90°,sinA=$\frac{3}{4}$,则cosB的值为( )| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
分析 根据一个角的余弦等于它余角的正弦,可得答案.
解答 解:由在Rt△ABC中,∠C=90°,得
∠A+∠B=90°,
cosB=sinA=$\frac{3}{4}$,
故选:D.
点评 本题考查了互余两角三角函数关系,利用一个角的余弦等于它余角的正弦是解题关键.

练习册系列答案
相关题目
17.已知a、b、c是△ABC的三边的长,且满足a2+b2+c2=ab+bc+ac,关于此三角形的形状有下列判断:①是锐角三角形;②是直角三角形;③是钝角三角形;④是等边三角形,其中正确说法的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
18.如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )


| A. | ①③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
2. 如图,在宽为20米,长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540平方米,设道路的宽为x米,则下列方程正确的是( )
如图,在宽为20米,长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540平方米,设道路的宽为x米,则下列方程正确的是( )
 如图,在宽为20米,长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540平方米,设道路的宽为x米,则下列方程正确的是( )
如图,在宽为20米,长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540平方米,设道路的宽为x米,则下列方程正确的是( )| A. | 32×20-20x-30x=540 | B. | 32×20-20x-30x-x2=540 | ||
| C. | (32-x)(20-x)=540 | D. | 32×20-20x-30x+2x2=540 |
12.已知直角三角形ABC中,斜边AB的长为m,∠B=50°,则直角边BC的长是( )
| A. | msin50° | B. | mtan50° | C. | mcos50° | D. | $\frac{m}{{tan{{50}°}}}$ |
19.把所有正偶数从小到大排列,并按如下规律分组:(2),(4,6),(8,10,12),(14,16,18,20),…,现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左往右数).如A2=(1,1),A10=(3,2),A18=(4,3),则A2018可表示为( )
| A. | (45,19) | B. | (45,20) | C. | (44,19) | D. | (44,20) |
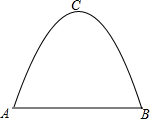 一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m. 已知二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+n(k≠0)的图象如图所示,下面有四个推断:
已知二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+n(k≠0)的图象如图所示,下面有四个推断: