题目内容
15.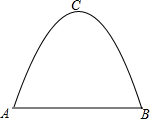 一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.(1)建立适当的平面直角坐标系,求抛物线的表达式;
(2)现有一辆货车的高度是4.4m,货车的宽度是2m,为了保证安全,车顶距离隧道顶部至少0.5m,通过计算说明这辆货车能否安全通过这条隧道.
分析 (1)以AB所在直线为x轴,以抛物线的对称轴为y轴建立平面直角坐标系xOy,如图所示,利用待定系数法即可解决问题.
(1)求出x=1时的y的值,与4.4+0.5比较即可解决问题.
解答 解:(1)本题答案不唯一,如:
以AB所在直线为x轴,以抛物线的对称轴为y轴建立平面直角坐标系xOy,如图所示.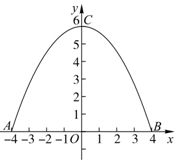
∴A(-4,0),B(4,0),C(0,6).
设这条抛物线的表达式为y=a(x-4)(x+4).
∵抛物线经过点C,
∴-16a=6.
∴a=-$\frac{3}{8}$
∴抛物线的表达式为y=-$\frac{3}{8}$x2+6,(-4≤x≤4).
(2)当x=1时,y=$\frac{45}{8}$,
∵4.4+0.5=4.9<$\frac{45}{8}$,
∴这辆货车能安全通过这条隧道.
点评 本题考查二次函数的应用、平面直角坐标系等知识,解题的关键是学会构建平面直角坐标系,掌握待定系数法解决问题,属于中考常考题型.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
3.有9名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前4名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这9名同学成绩的( )
| A. | 中位数 | B. | 众数 | C. | 平均数 | D. | 加权平均数 |
20.从单词“hello”中随机抽取一个字母,抽中l的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
7.已知:在Rt△ABC中,∠C=90°,sinA=$\frac{3}{4}$,则cosB的值为( )
| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
5.下列计算正确的是( )
| A. | -$\frac{1}{2}$+$\frac{1}{3}$=$\frac{1}{6}$ | B. | 2x2y+xy2=3x2y | ||
| C. | -2(xy-$\frac{1}{2}$x2y)=-2xy-x2y | D. | $\frac{x-1}{2}$-1=$\frac{x+1}{3}$去分母得3(x-1)-6=2(x+1) |
 如图,点A,B,C,D,E为⊙O的五等分点,动点M从圆心O出发,沿线段OA→劣弧AC→线段CO的路线做匀速运动,设运动的时间为t,∠DME的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )
如图,点A,B,C,D,E为⊙O的五等分点,动点M从圆心O出发,沿线段OA→劣弧AC→线段CO的路线做匀速运动,设运动的时间为t,∠DME的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )


