题目内容
5.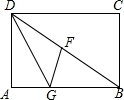 如图,四边形ABCD是矩形,DG平分∠ADE交AB于点G,GF⊥BD,垂足为F.
如图,四边形ABCD是矩形,DG平分∠ADE交AB于点G,GF⊥BD,垂足为F.(1)求证:△AGD≌△FGD;
(2)若AB=8,BC=6,求AG的长.
分析 (1)由矩形的性质和已知条件得出∠A=∠GFD,∠ADG=∠FDG,由AAS即可证明△AGD≌△FGD;
(2)由勾股定理求出BD,由△AGD≌△FGD,得出对应边相等AD=DF=6,FG=AG,求出BF,设AG=FG=x,则BG=8-x,在Rt△BFG中,由勾股定理得出方程,解方程即可.
解答 (1)证明:∵四边形ABCD是矩形,GF⊥BD,
∴∠A=90°,∠GFD=90°,
∴∠A=∠GFD,
∵DG平分∠ADB,
∴∠ADG=∠FDG,
在△AGD和△FGD中,$\left\{\begin{array}{l}{∠A=∠GFD}&{\;}\\{∠ADG=∠FDG}&{\;}\\{DG=DG}&{\;}\end{array}\right.$,
∴△AGD≌△FGD(AAS);
(2)解:∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=6,
根据勾股定理得:BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵△AGD≌△FGD,
∴AD=DF=6,FG=AG,
∴BF=BD-DF=4,
设AG=FG=x,则BG=8-x,
在Rt△BFG中,FG2+BF2=BG2,
即x2+42=(8-x)2,
解得:x=3,
∴AG=3.
点评 本题考查了矩形的性质、全等三角形的判定与性质、勾股定理;熟练掌握矩形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.计算3-1的结果是( )
| A. | -1 | B. | -3 | C. | 3 | D. | $\frac{1}{3}$ |
14.直线y=2x+3与坐标轴围成的面积是( )
| A. | $\frac{3}{4}$ | B. | 3 | C. | $\frac{9}{4}$ | D. | 6 |
10. 如图,△ABC是⊙O的内接三角形,∠OAB=35°,则∠ACB的度数为( )
如图,△ABC是⊙O的内接三角形,∠OAB=35°,则∠ACB的度数为( )
 如图,△ABC是⊙O的内接三角形,∠OAB=35°,则∠ACB的度数为( )
如图,△ABC是⊙O的内接三角形,∠OAB=35°,则∠ACB的度数为( )| A. | 35° | B. | 55° | C. | 60° | D. | 70° |
 如图,已知AB∥CD,EF平分∠AEG,∠EFG=50°,则∠EGF的度数是80°.
如图,已知AB∥CD,EF平分∠AEG,∠EFG=50°,则∠EGF的度数是80°.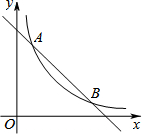 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(k≠0)经过A、B两点,A、B两点的横坐标分别为1和4,直线AB与y轴所夹锐角为45°.则k=4.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(k≠0)经过A、B两点,A、B两点的横坐标分别为1和4,直线AB与y轴所夹锐角为45°.则k=4.