题目内容
14．直线y=2x+3与坐标轴围成的面积是（ ）| A． | $\frac{3}{4}$ | B． | 3 | C． | $\frac{9}{4}$ | D． | 6 |
分析 设直线与x轴、y轴分别交于A、B两点，可求得A、B两点的坐标，可求得△AOB的面积．
解答 解：如图，设直线与x轴、y轴分别交于A、B两点，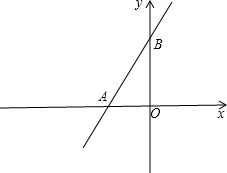
在y=2x+3中，令y=0，可得2x+3=0，解得x=-$\frac{3}{2}$，令x=0，可得y=3，
∴A（$\frac{3}{2}$，0），B（0，3），
∴OA=$\frac{3}{2}$，OB=3，
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×$\frac{3}{2}$×3=$\frac{9}{4}$，
故选C．
点评 本题主要考查一次函数与坐标轴的交点，掌握函数与坐标轴的交点坐标的求法是解题的关键．
练习册系列答案
相关题目
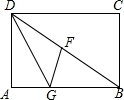如图，四边形ABCD是矩形，DG平分∠ADE交AB于点G，GF⊥BD，垂足为F．
如图，点A在双曲线y=$\frac{k}{x}$上，AB⊥x轴于B，AC⊥y轴于C，且△ABC的面积为2，则k=-4．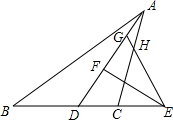
如图，在△ABC中，2AB=3AC，AD为△BAC的角平分线，点H在线段AC上，且CH=2AH，E为BC延长线上的一点，连接EH并延长交AD于点G，使EG=ED，过点E作EF⊥AD于点F，则AG：FG=4：7．
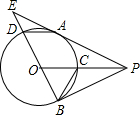如图，P为⊙O外一点，PA、PB分别切⊙O于A、B两点，OP交⊙O于点C，连接BO并延长交⊙O于点D，交PA的延长线于点E，连接AD、BC．下列结论：①AD∥PO；②△ADE∽△PCB；③tan∠EAD=$\frac{ED}{EA}$；④BD2=2AD•OP．其中一定正确的是（ ）