题目内容
13.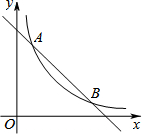 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(k≠0)经过A、B两点,A、B两点的横坐标分别为1和4,直线AB与y轴所夹锐角为45°.则k=4.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(k≠0)经过A、B两点,A、B两点的横坐标分别为1和4,直线AB与y轴所夹锐角为45°.则k=4.
分析 分别过A、B两点作x轴的垂线,垂足分别为C、D,过B作BE⊥y轴垂足为E,交AC于F,由A、B两点的横坐标,可表示出其纵坐标,结合条件可得到AF=BF,可得到关于k的方程,可求得k的值.
解答 解:
如图,分别过A、B两点作x轴的垂线,垂足分别为C、D,过B作BE⊥y轴,垂足为E,交AC于点F,
∵A、B两点的横坐标分别为1和4,且A、B两点在y=$\frac{k}{x}$的图象上,
∴A、B两点的纵坐标分别为k和$\frac{k}{4}$,
∴BE=4,EF=1,AC=k,BD=$\frac{k}{4}$,
∴BF=BE-EF=3,AF=AC-BD=k-$\frac{k}{4}$=$\frac{3}{4}$k,
∵直线AB与y轴的夹角为45°,
∴∠FAB=45°,
∴AF=BF,
∴$\frac{3}{4}$k=3,解得k=4,
故答案为:4.
点评 本题主要考查一次函数与反比例函数的交点问题,用k分别表示出AF和BF是解题的关键,注意充分利用点的坐标与函数解析式的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.3.14159、-$\root{3}{343}$、0.13113113、-π这四个实数中无理数的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 | ||||
| E. | 4 |
1.下列各式计算不正确的是( )
| A. | 22•23=25 | B. | ${(-2)^{-1}}=-\frac{1}{2}$ | C. | (25)5=225 | D. | $\sqrt{(1-\sqrt{2}{)^2}}=1-\sqrt{2}$ |
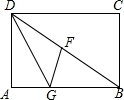 如图,四边形ABCD是矩形,DG平分∠ADE交AB于点G,GF⊥BD,垂足为F.
如图,四边形ABCD是矩形,DG平分∠ADE交AB于点G,GF⊥BD,垂足为F.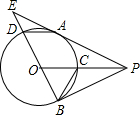 如图,P为⊙O外一点,PA、PB分别切⊙O于A、B两点,OP交⊙O于点C,连接BO并延长交⊙O于点D,交PA的延长线于点E,连接AD、BC.下列结论:①AD∥PO;②△ADE∽△PCB;③tan∠EAD=$\frac{ED}{EA}$;④BD2=2AD•OP.其中一定正确的是( )
如图,P为⊙O外一点,PA、PB分别切⊙O于A、B两点,OP交⊙O于点C,连接BO并延长交⊙O于点D,交PA的延长线于点E,连接AD、BC.下列结论:①AD∥PO;②△ADE∽△PCB;③tan∠EAD=$\frac{ED}{EA}$;④BD2=2AD•OP.其中一定正确的是( )