题目内容
15.化简求值:(a-b+$\frac{4ab}{a-b}$)•(a+b-$\frac{4ab}{a+b}$),其中a=$\frac{3}{2}$,b=-$\frac{1}{2}$.分析 原式括号中两项通分并利用同分母分式的加减法则计算,约分得到最简结果,把a与b的值代入计算即可求出值.
解答 解:原式=$\frac{(a-b)^{2}+4ab}{a-b}$•$\frac{(a+b)^{2}-4ab}{a+b}$=$\frac{(a+b)^{2}(a-b)^{2}}{(a+b)(a-b)}$=a2-b2,
当a=$\frac{3}{2}$,b=-$\frac{1}{2}$时,原式=$\frac{9}{4}$-$\frac{1}{4}$=2.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3.3.14159、-$\root{3}{343}$、0.13113113、-π这四个实数中无理数的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 | ||||
| E. | 4 |
10.下列说法正确的是( )
| A. | -a的绝对值是a | B. | 若|x|=-x,则x是负数 | ||
| C. | a的绝对值是a | D. | 若m=-n,则|m|=|n| |

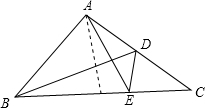 已知在△ABC中,∠BAC=90°,AB=AC,D是AC的中点,AE⊥BD交BC于E,求证:BD=AE+DE.(提示:过点A作BC的垂线交BD于H)
已知在△ABC中,∠BAC=90°,AB=AC,D是AC的中点,AE⊥BD交BC于E,求证:BD=AE+DE.(提示:过点A作BC的垂线交BD于H)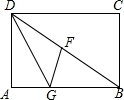 如图,四边形ABCD是矩形,DG平分∠ADE交AB于点G,GF⊥BD,垂足为F.
如图,四边形ABCD是矩形,DG平分∠ADE交AB于点G,GF⊥BD,垂足为F.