题目内容
19.解方程(组)(1)$\left\{\begin{array}{l}x-3y=1\\ 2y-x=-5\end{array}\right.$
(2)$\frac{1}{2x-3}$+$\frac{x}{3-2x}$=-2.
分析 (1)方程组利用加减消元法求出解即可;
(2)分式方程去分母转化为整式整式,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)$\left\{\begin{array}{l}{x-3y=1①}\\{2y-x=-5②}\end{array}\right.$,
①+②得:-y=-4,
解得:y=4,
把y=4代入①得:x=13,
则方程组的解为$\left\{\begin{array}{l}{x=13}\\{y=4}\end{array}\right.$;
(2)去分母得:1-x=-4x+6,
解得:x=$\frac{5}{3}$,
经检验x=$\frac{5}{3}$是分式方程的解.
点评 此题考查了解分式方程,以及解二元一次方程组,解分式方程利用了转化的思想,解分式方程注意要检验.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
9. 如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则DF:FB等于( )
如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则DF:FB等于( )
 如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则DF:FB等于( )
如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则DF:FB等于( )| A. | 1:1 | B. | 1:2 | C. | 1:3 | D. | 2:3 |
14. 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | ∠2与∠1是同位角 | B. | ∠C与∠1是内错角 | ||
| C. | ∠2与∠3是同旁内角 | D. | ∠B与∠3是同位角 |
8.下列选项中∠1与∠2不是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
19.已知P=$\frac{7}{17}$m-1,Q=m2-$\frac{10}{17}$m(m为任意实数),则P与Q的大小关系为( )
| A. | P>Q | B. | P=Q | C. | P<Q | D. | 不能确定 |
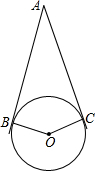 如图,AB、AC与⊙O相切于B、C两点,∠A=40°,点P是圆上异于B、C的一动点,则∠BPC=70或110度.
如图,AB、AC与⊙O相切于B、C两点,∠A=40°,点P是圆上异于B、C的一动点,则∠BPC=70或110度.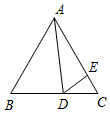 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=4,CE=$\frac{4}{3}$,则△ABC的面积为9$\sqrt{3}$.
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=4,CE=$\frac{4}{3}$,则△ABC的面积为9$\sqrt{3}$.