题目内容
10.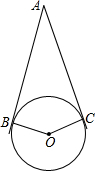 如图,AB、AC与⊙O相切于B、C两点,∠A=40°,点P是圆上异于B、C的一动点,则∠BPC=70或110度.
如图,AB、AC与⊙O相切于B、C两点,∠A=40°,点P是圆上异于B、C的一动点,则∠BPC=70或110度.
分析 根据切线的性质求出∠ABO=∠ACO=90°,求出∠BOC,分为两种情况,求出P在优弧上时的∠BPC,即可求出P在劣弧上的∠BPC.
解答 解:∵AB、AC与⊙O相切于B、C两点,
∴OB⊥AB,OC⊥AC,
∴∠ABO=∠ACO=90°,
∵∠A=40°,
∴∠BOC=360°-90°-90°-40°=140°,
当P在优弧BC上时,∠BP1C=$\frac{1}{2}$∠BOC=70°,
当P在劣弧BC上时,∠BP2C=180°-70°=110°,
故答案为:70或110.
点评 本题考查圆的切线性质,在解题过程中还要注意对圆的内接四边形、圆周角、圆心角的有关性质的综合应用.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
15.下列说法中,不正确的是( )
| A. | 0既不是正数,也不是负数 | |
| B. | 最小的有理数是0 | |
| C. | 绝对值最小的有理数是0 | |
| D. | 除以一个不为0的数等于乘以这个数的倒数 |
20. 如图,过四边形ABCD的四个顶点分别作对角线AC,BD的平行线,所围成的四边形EFGH显然是平行四边形.
如图,过四边形ABCD的四个顶点分别作对角线AC,BD的平行线,所围成的四边形EFGH显然是平行四边形.
(1)当四边形ABCD分别是菱形、矩形、平行四边形时,相应的四边形EFGH一定是“平行四边形、菱形、矩形、正方形”中的哪一种?请将你的结论填入下表:
(2)反之,当用上述方法所围成的平行四边形EFGH分别是矩形、菱形时,相应的原四边形ABCD必须满足怎样的条件?当对角线互相垂直时,四边形EFGH是矩形; 当对角线相等时四边形EFGH是菱形.
 如图,过四边形ABCD的四个顶点分别作对角线AC,BD的平行线,所围成的四边形EFGH显然是平行四边形.
如图,过四边形ABCD的四个顶点分别作对角线AC,BD的平行线,所围成的四边形EFGH显然是平行四边形.(1)当四边形ABCD分别是菱形、矩形、平行四边形时,相应的四边形EFGH一定是“平行四边形、菱形、矩形、正方形”中的哪一种?请将你的结论填入下表:
| 四边形ABCD | 菱形 | 矩形 | 平行四边形 |
| 四边形EFGH | 矩形 | 菱形 | 平行四边形 |
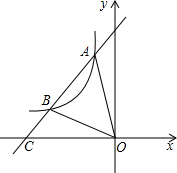 如图,直线y1=kx+b与反比例函数y2=$\frac{k′}{x}$(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
如图,直线y1=kx+b与反比例函数y2=$\frac{k′}{x}$(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.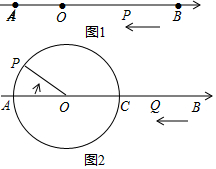 如图1,已知点A,B在以O为原点的数轴上表示的数分别为a,b,且a,b满足|a+4|+(b-10)2=0,动点P从点B出发沿射线BA运动.
如图1,已知点A,B在以O为原点的数轴上表示的数分别为a,b,且a,b满足|a+4|+(b-10)2=0,动点P从点B出发沿射线BA运动.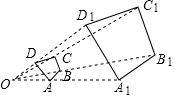 如图,点O为四边形ABCD与四边形A1B1C1D1的位似中心,OA1=3OA,若四边形ABCD的面积为5,则四边形A1B1C1D1的面积为45.
如图,点O为四边形ABCD与四边形A1B1C1D1的位似中心,OA1=3OA,若四边形ABCD的面积为5,则四边形A1B1C1D1的面积为45.