题目内容
7.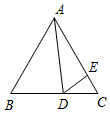 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=4,CE=$\frac{4}{3}$,则△ABC的面积为9$\sqrt{3}$.
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=4,CE=$\frac{4}{3}$,则△ABC的面积为9$\sqrt{3}$.
分析 首先由△ABC是等边三角形,可得∠B=∠C=∠ADE=60°,又由三角形外角的性质,求得∠ADB=∠DEC,即可得△ABD∽△DCE,又由BD=4,CE=$\frac{4}{3}$,根据相似三角形的对应边成比例,即可求得AB的长,则可求得△ABC的面积.
解答 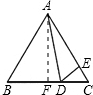 解:∵△ABC是等边三角形,∠ADE=60°,
解:∵△ABC是等边三角形,∠ADE=60°,
∴∠B=∠C=∠ADE=60°,AB=BC,
∵∠ADB=∠DAC+∠C,∠DEC=∠ADE+∠DAC,
∴∠ADB=∠DEC,
∴△ABD∽△DCE,
∴$\frac{AB}{DC}$=$\frac{BD}{CE}$,
∵BD=4,CE=$\frac{4}{3}$,
设AB=x,则DC=x-4,
∴$\frac{x}{x-4}$=$\frac{4}{\frac{4}{3}}$,
∴x=6,
∴AB=6,
过点A作AF⊥BC于F,
在Rt△ABF中,AF=AB•sin60°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$BC•AF=$\frac{1}{2}$×6×3$\sqrt{3}$=9$\sqrt{3}$.
故答案为:9$\sqrt{3}$.
点评 此题考查了相似三角形的判定与性质与等边三角形的性质.此题综合性较强,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
17.在数-2.5,5$\frac{1}{2}$,0,$\frac{π}{2}$,-1.121121112…,-0.0$\stackrel{•}{5}$中,无理数的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
15.下列说法中,不正确的是( )
| A. | 0既不是正数,也不是负数 | |
| B. | 最小的有理数是0 | |
| C. | 绝对值最小的有理数是0 | |
| D. | 除以一个不为0的数等于乘以这个数的倒数 |
12.下列运动过程能表示“平移”的是( )
| A. | 高层住宅电梯的上下运动 | B. | 电风扇叶片的转动 | ||
| C. | 钟表上时针的运动 | D. | 地面上沿直线滚动的足球 |
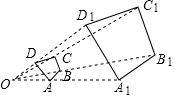 如图,点O为四边形ABCD与四边形A1B1C1D1的位似中心,OA1=3OA,若四边形ABCD的面积为5,则四边形A1B1C1D1的面积为45.
如图,点O为四边形ABCD与四边形A1B1C1D1的位似中心,OA1=3OA,若四边形ABCD的面积为5,则四边形A1B1C1D1的面积为45.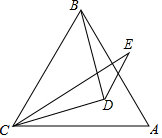 如图,在△ABC中,AB=AC=BC,在△ABC内取一点D,使DB=DC,又作∠ECD=∠ACD,且AC=EC,试问∠BAC与∠E的数量关系如何?请说明理由.
如图,在△ABC中,AB=AC=BC,在△ABC内取一点D,使DB=DC,又作∠ECD=∠ACD,且AC=EC,试问∠BAC与∠E的数量关系如何?请说明理由.