题目内容
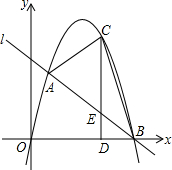 如图,抛物线y=ax2+bx与直线l交于点A(1,5)、B(6,0),点C是l上方的抛物线上的一动点,过C作CD⊥x轴于点D,交直线l于点E.连结AC、BC.
如图,抛物线y=ax2+bx与直线l交于点A(1,5)、B(6,0),点C是l上方的抛物线上的一动点,过C作CD⊥x轴于点D,交直线l于点E.连结AC、BC.(1)求抛物线的解析式;
(2)设点C的横坐标为n,△ABC的面积为S,求出S的最大值;
(3)在抛物线上是否存在点P,使得△PAB是直角三角形,且始终满足AB边为直角边?若存在,求出所有符合条件的P的坐标;若不存在,简要说明理由.
考点:二次函数综合题
专题:
分析:(1)将点A(1,5)、B(6,0)代入y=ax2+bx,运用待定系数法即可求出抛物线的解析式为y=-x2+6x;
(2)先由待定系数法求出直线l的解析式为y=-x+6,设C(n,-n2+6n),E(n,-n+6),则EC=(-n2+6n)-(-n+6)=-n2+7n-6,再过A作AF⊥CD于F,则AF=n-1,DB=6-n,根据S=S△ACE+S△BCE得出S=-
n2+
n-15,再利用配方法写成顶点式,即可求出S的最大值;
(3)分两种情况进行讨论:①当∠PBA=90°时,先求出过点B且垂直于AB的直线解析式为y=x-6,再解方程组
,可得P1(-1,-7);②当∠PAB=90°时,先求出过点A且垂直于AB的直线解析式为y=x+4,再解方程组
,可得P2(4,8).
(2)先由待定系数法求出直线l的解析式为y=-x+6,设C(n,-n2+6n),E(n,-n+6),则EC=(-n2+6n)-(-n+6)=-n2+7n-6,再过A作AF⊥CD于F,则AF=n-1,DB=6-n,根据S=S△ACE+S△BCE得出S=-
| 5 |
| 2 |
| 35 |
| 2 |
(3)分两种情况进行讨论:①当∠PBA=90°时,先求出过点B且垂直于AB的直线解析式为y=x-6,再解方程组
|
|
解答:解:(1)∵抛物线y=ax2+bx与直线l交于点A(1,5)、B(6,0),
∴
,解得
,
∴抛物线的解析式为y=-x2+6x;
 (2)易求直线l的解析式为y=-x+6.
(2)易求直线l的解析式为y=-x+6.
由题意,知C(n,-n2+6n),E(n,-n+6),
∴EC=(-n2+6n)-(-n+6),即EC=-n2+7n-6.
过A作AF⊥CD于F,则AF=n-1,DB=6-n,
∴S=S△ACE+S△BCE
=
×EC×(n-1)+
×EC×(6-n)
=
×EC×5=
(-n2+7n-6),
即S=-
n2+
n-15,
配方得S=-
(n-
)2+
.
∵-
<0,
∴S有最大值,当n=
时,S最大值=
;
(3)在抛物线上存在点P,能够使得△PAB是直角三角形,且始终满足AB边为直角边.分两种情况:
①当∠PBA=90°时,
∵∠ABO=45°,
∴过点B且垂直于AB的直线解析式为y=x-6,
解方程组
,得
,
,
∵B(6,0),
∴P1(-1,-7);
②当∠PAB=90°时,
∵过点A且垂直于AB的直线解析式为y=x+4,
解方程组
,得
,
,
∵A(1,5),
∴P2(4,8).
综上所述,符合条件的P点坐标为P1(-1,-7),P2(4,8).
∴
|
|
∴抛物线的解析式为y=-x2+6x;
 (2)易求直线l的解析式为y=-x+6.
(2)易求直线l的解析式为y=-x+6.由题意,知C(n,-n2+6n),E(n,-n+6),
∴EC=(-n2+6n)-(-n+6),即EC=-n2+7n-6.
过A作AF⊥CD于F,则AF=n-1,DB=6-n,
∴S=S△ACE+S△BCE
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 5 |
| 2 |
即S=-
| 5 |
| 2 |
| 35 |
| 2 |
配方得S=-
| 5 |
| 2 |
| 7 |
| 2 |
| 125 |
| 8 |
∵-
| 5 |
| 2 |
∴S有最大值,当n=
| 7 |
| 2 |
| 125 |
| 8 |
(3)在抛物线上存在点P,能够使得△PAB是直角三角形,且始终满足AB边为直角边.分两种情况:
①当∠PBA=90°时,
∵∠ABO=45°,
∴过点B且垂直于AB的直线解析式为y=x-6,
解方程组
|
|
|
∵B(6,0),
∴P1(-1,-7);
②当∠PAB=90°时,
∵过点A且垂直于AB的直线解析式为y=x+4,
解方程组
|
|
|
∵A(1,5),
∴P2(4,8).
综上所述,符合条件的P点坐标为P1(-1,-7),P2(4,8).
点评:本题是二次函数的综合题型,其中涉及到运用待定系数法求二次函数、一次函数的解析式,三角形的面积求法,二次函数的性质,互相垂直的两直线斜率之积为-1,两函数交点坐标的求法等知识,综合性较强,难度适中.运用数形结合、分类讨论及方程思想是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
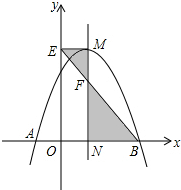 如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F,已知点A的坐标为(-1,0).
如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F,已知点A的坐标为(-1,0). 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx-4与x轴交于点A(-2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx-4与x轴交于点A(-2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴. 如图,已知两个反比例函数
如图,已知两个反比例函数