题目内容
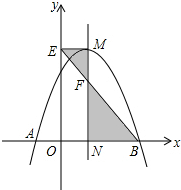 如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F,已知点A的坐标为(-1,0).
如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F,已知点A的坐标为(-1,0).(1)求该抛物线的解析式及顶点M的坐标.
(2)求△EMF与△BNF的面积之比.
考点:抛物线与x轴的交点,二次函数的性质,待定系数法求二次函数解析式,相似三角形的判定与性质
专题:代数几何综合题
分析:(1)直接将(-1,0)代入求出即可,再利用配方法求出顶点坐标;
(2)利用EM∥BN,则△EMF∽△BNF,进而求出△EMF与△BNE的面积之比.
(2)利用EM∥BN,则△EMF∽△BNF,进而求出△EMF与△BNE的面积之比.
解答:解:(1)由题意可得:-(-1)2+2×(-1)+c=0,
解得:c=3,
∴y=-x2+2x+3,
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点M(1,4);
(2)∵A(-1,0),抛物线的对称轴为直线x=1,
∴点B(3,0),
∴EM=1,BN=2,
∵EM∥BN,
∴△EMF∽△BNF,
∴
=(
)2=(
)2=
.
解得:c=3,
∴y=-x2+2x+3,
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点M(1,4);
(2)∵A(-1,0),抛物线的对称轴为直线x=1,
∴点B(3,0),
∴EM=1,BN=2,
∵EM∥BN,
∴△EMF∽△BNF,
∴
| S△EMF |
| S△BNF |
| EM |
| BN |
| 1 |
| 2 |
| 1 |
| 4 |
点评:此题主要考查了待定系数法求二次函数解析式以及相似三角形的判定与性质,得出△EMF∽△BNF是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
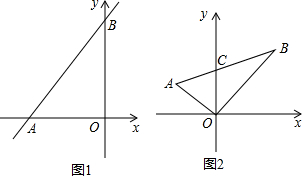 如图1,在平面直角坐标系中,直线AB分别交x轴y轴于A、B两点.设∠OAB=a°,∠OBA=b°,且
如图1,在平面直角坐标系中,直线AB分别交x轴y轴于A、B两点.设∠OAB=a°,∠OBA=b°,且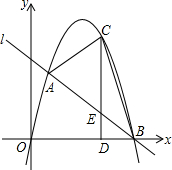 如图,抛物线y=ax2+bx与直线l交于点A(1,5)、B(6,0),点C是l上方的抛物线上的一动点,过C作CD⊥x轴于点D,交直线l于点E.连结AC、BC.
如图,抛物线y=ax2+bx与直线l交于点A(1,5)、B(6,0),点C是l上方的抛物线上的一动点,过C作CD⊥x轴于点D,交直线l于点E.连结AC、BC. 如图,平面上的6个点可以构成5个正三角形,若在此基础上,再增加10个正三角形,那么至少还需添加
如图,平面上的6个点可以构成5个正三角形,若在此基础上,再增加10个正三角形,那么至少还需添加