题目内容
 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx-4与x轴交于点A(-2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx-4与x轴交于点A(-2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.(1)求抛物线的解析式;
(2)若两动点M,H分别从点A,B以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到达原点时,点H立刻掉头并以每秒
| 3 |
| 2 |
考点:二次函数综合题
专题:压轴题
分析:(1)根据抛物线y=ax2+bx-4与x轴交于点A(-2,0),直线x=1是该抛物线的对称轴,得到方程组
,解方程组即可求出抛物线的解析式;
(2)由于点M到达抛物线的对称轴时需要3秒,所以t≤3,又当点M到达原点时需要2秒,且此时点H立刻掉头,所以可分两种情况进行讨论:①当0<t≤2时,由△AMP∽△AOC,得出比例式,求出PM,AH,根据三角形的面积公式求出即可;②当2<t≤3时,过点P作PM⊥x轴于M,PF⊥y轴于点F,求出PM,AH,根据三角形面积公式求解,利用配方法求出最值即可.
|
(2)由于点M到达抛物线的对称轴时需要3秒,所以t≤3,又当点M到达原点时需要2秒,且此时点H立刻掉头,所以可分两种情况进行讨论:①当0<t≤2时,由△AMP∽△AOC,得出比例式,求出PM,AH,根据三角形的面积公式求出即可;②当2<t≤3时,过点P作PM⊥x轴于M,PF⊥y轴于点F,求出PM,AH,根据三角形面积公式求解,利用配方法求出最值即可.
解答:解:(1)∵抛物线y=ax2+bx-4与x轴交于点A(-2,0),直线x=1是该抛物线的对称轴,
∴
,
解得:
,
∴抛物线的解析式是:y=
x2-x-4,
 (2)分两种情况:
(2)分两种情况:
①当0<t≤2时,
∵PM∥OC,
∴△AMP∽△AOC,
∴
=
,即
=
,
∴PM=2t.
解方程
x2-x-4=0,得x1=-2,x2=4,
∵A(-2,0),
∴B(4,0),
∴AB=4-(-2)=6.
∵AH=AB-BH=6-t,
∴S=
PM•AH=
×2t(6-t)=-t2+6t=-(t-3)2+9,
 当t=2时S的最大值为8;
当t=2时S的最大值为8;
②当2<t≤3时,过点P作PM⊥x轴于M,作PF⊥y轴于点F,则△COB∽△CFP,
又∵将x=0代入抛物线求得C点坐标为(0,-4),
∴CO=OB,
∴FP=FC=t-2,PM=4-(t-2)=6-t,AH=4+
(t-2)=
t+1,
∴S=
PM•AH=
(6-t)(
t+1)=-
t2+4t+3=-
(t-
)2+
,
当t=
时,S最大值为
.
综上所述,点M的运动时间t与△APH面积S的函数关系式是S=
,S的最大值为
.
∴
|
解得:
|
∴抛物线的解析式是:y=
| 1 |
| 2 |
 (2)分两种情况:
(2)分两种情况:①当0<t≤2时,
∵PM∥OC,
∴△AMP∽△AOC,
∴
| PM |
| OC |
| AM |
| AO |
| PM |
| 4 |
| t |
| 2 |
∴PM=2t.
解方程
| 1 |
| 2 |
∵A(-2,0),
∴B(4,0),
∴AB=4-(-2)=6.
∵AH=AB-BH=6-t,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
 当t=2时S的最大值为8;
当t=2时S的最大值为8;②当2<t≤3时,过点P作PM⊥x轴于M,作PF⊥y轴于点F,则△COB∽△CFP,
又∵将x=0代入抛物线求得C点坐标为(0,-4),
∴CO=OB,
∴FP=FC=t-2,PM=4-(t-2)=6-t,AH=4+
| 3 |
| 2 |
| 3 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 8 |
| 3 |
| 25 |
| 3 |
当t=
| 8 |
| 3 |
| 25 |
| 3 |
综上所述,点M的运动时间t与△APH面积S的函数关系式是S=
|
| 25 |
| 3 |
点评:本题是二次函数的综合题型,其中涉及到运用待定系数法求二次函数的解析式,三角形的面积,二次函数的最值等知识,综合性较强,难度适中.运用数形结合、分类讨论及方程思想是解题的关键.

练习册系列答案
相关题目
已知x,y满足关系式2x+y=9和x+2y=6,则x+y=( )
| A、6 | B、-1 | C、15 | D、5 |
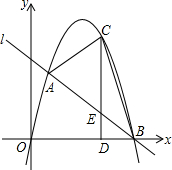 如图,抛物线y=ax2+bx与直线l交于点A(1,5)、B(6,0),点C是l上方的抛物线上的一动点,过C作CD⊥x轴于点D,交直线l于点E.连结AC、BC.
如图,抛物线y=ax2+bx与直线l交于点A(1,5)、B(6,0),点C是l上方的抛物线上的一动点,过C作CD⊥x轴于点D,交直线l于点E.连结AC、BC.
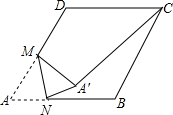 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是
如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是