题目内容
 如图,已知两个反比例函数y1=
如图,已知两个反比例函数y1=| k1 |
| x |
| k2 |
| x |
| k1 |
| x |
| k2 |
| x |
| k2 |
| x |
| k1 |
| x |
(1)用含k1、k2的代数式表示四边形ACOB的面积为:S四边形ACOB=
(2)当k1=8,k2=2时,若点A横坐标为2,求梯形ACBD的两条对角线的交点F的坐标.
考点:反比例函数综合题,待定系数法求一次函数解析式,反比例函数系数k的几何意义
专题:
分析:(1)利用反比例函数的比例系数的几何意义可以表示S△CHO、S△OGB、S矩形AGOH,进而表示出S四边形ACOB.
(2)由于点A、B、C、D的坐标密切相关,由点A的横坐标为2可以求出这4个点的坐标.F的横坐标与点A横坐标相同,都为2,只需求出直线CD的解析式,就可求出点F的坐标.
(2)由于点A、B、C、D的坐标密切相关,由点A的横坐标为2可以求出这4个点的坐标.F的横坐标与点A横坐标相同,都为2,只需求出直线CD的解析式,就可求出点F的坐标.
解答:解:(1)由题可知:AG∥y轴,AH∥x轴,点A在反比例函数y1=
的图象上,点B、C在反比例函数y2=
图象上,
由反比例函数的比例系数的几何意义可得:S△CHO=S△OGB=
k2,S矩形AGOH=k1.
∴S四边形ACOB=S矩形AGOH-S△CHO-S△OGB=k1-k2.
故答案为:k1-k2.
(2)设点A的坐标为(2,b),点A在反比例函数y1=
的图象上,
∴2b=8.
∴b=4.
∴点A的坐标为(2,4).
∵AC∥x轴,
∴点C的纵坐标为4.
∵点C在反比例函数y2=
的图象上,
∴点C的横坐标为
.
∴点C的坐标为(
,4).
同理:点B的坐标为(2,1),点D的坐标为(8,1).
设直线CD的解析式为y=mx+n.
则
,
解得
.
则直线CD的解析式为y=-
x+
.
∵AF∥y轴,
∴xF=xA=2.
∴yF=-
×2+
=
.
∴梯形ACBD的两条对角线的交点F的坐标为(2,
).
| k1 |
| x |
| k2 |
| x |
由反比例函数的比例系数的几何意义可得:S△CHO=S△OGB=
| 1 |
| 2 |
∴S四边形ACOB=S矩形AGOH-S△CHO-S△OGB=k1-k2.
故答案为:k1-k2.
(2)设点A的坐标为(2,b),点A在反比例函数y1=
| 8 |
| x |
∴2b=8.
∴b=4.
∴点A的坐标为(2,4).
∵AC∥x轴,
∴点C的纵坐标为4.
∵点C在反比例函数y2=
| 2 |
| x |
∴点C的横坐标为
| 1 |
| 2 |
∴点C的坐标为(
| 1 |
| 2 |
同理:点B的坐标为(2,1),点D的坐标为(8,1).
设直线CD的解析式为y=mx+n.
则
|
解得
|
则直线CD的解析式为y=-
| 2 |
| 5 |
| 21 |
| 5 |
∵AF∥y轴,
∴xF=xA=2.
∴yF=-
| 2 |
| 5 |
| 21 |
| 5 |
| 17 |
| 5 |
∴梯形ACBD的两条对角线的交点F的坐标为(2,
| 17 |
| 5 |
点评:考查了反比例函数综合题,在选择题或填空题中,涉及到与反比例函数有关的面积问题时,运用反比例函数的比例系数的几何意义来解比较方便.至于第二小题,除了通过求直线CD的解析式来求点F的坐标外,还可以先证明△CAF~△DBF,再运用相似三角形的性质求出FB长,进而求出点F的坐标.

练习册系列答案
相关题目
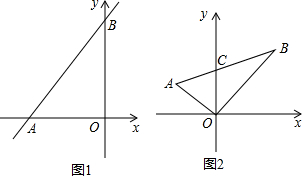 如图1,在平面直角坐标系中,直线AB分别交x轴y轴于A、B两点.设∠OAB=a°,∠OBA=b°,且
如图1,在平面直角坐标系中,直线AB分别交x轴y轴于A、B两点.设∠OAB=a°,∠OBA=b°,且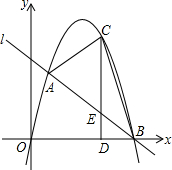 如图,抛物线y=ax2+bx与直线l交于点A(1,5)、B(6,0),点C是l上方的抛物线上的一动点,过C作CD⊥x轴于点D,交直线l于点E.连结AC、BC.
如图,抛物线y=ax2+bx与直线l交于点A(1,5)、B(6,0),点C是l上方的抛物线上的一动点,过C作CD⊥x轴于点D,交直线l于点E.连结AC、BC.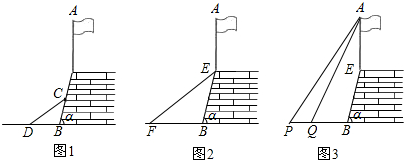
 如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=
如图,点B、E、C、F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=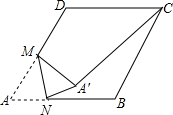 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是
如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 如图,平面上的6个点可以构成5个正三角形,若在此基础上,再增加10个正三角形,那么至少还需添加
如图,平面上的6个点可以构成5个正三角形,若在此基础上,再增加10个正三角形,那么至少还需添加 如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.
如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.