题目内容
如图1,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,点D是BC上一定点.动点P从C出发,以2cm/s的速度沿C→A→B方向运动,动点Q从D出发,以1cm/s的速度沿D→B方向运动.点P出发5s后,点Q才开始出发,且当一个点达到B时,另一个点随之停止.图2是当0≤t≤5时△BPQ的面积S(cm2)与点P的运动时间t(s)的函数图象.
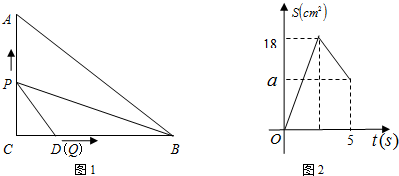
(1)CD= ,a= ;
(2)当点P在边AB上时,为何值时,使得△BPQ与△ABC为相似?
(3)运动过程中,求出当△BPQ是以BP为腰的等腰三角形时t的值.

(1)CD=
(2)当点P在边AB上时,为何值时,使得△BPQ与△ABC为相似?
(3)运动过程中,求出当△BPQ是以BP为腰的等腰三角形时t的值.
考点:相似形综合题,动点问题的函数图象,勾股定理的应用
专题:综合题
分析:(1)根据函数图象得到当点P运动到点A时,△BPQ的面积为18,利用三角形面积公式可计算出BD=6,则CD=2,当t=5s时,AP=4,点Q在D点,作PH⊥BC于H,在Rt△ABC中根据勾股定理计算出AB=10,再证明△BPH∽△BAC,利用相似比计算出PH,然后根据三角形面积公式得到S△PBQ,即a=S△PBQ;
(2)分类讨论:当3<t≤5,点Q在D点,BP=16-2t,若PD⊥BC得到△BPQ∽△BAC,利用相似比得t值;当5<t≤8,DQ=t-5,BQ=11-t,BP=16-2t,当∠PQB=90°时,△BPQ∽△BAC,利用相似比得t值;当∠BPQ=90°时,△BPQ∽△BAC,利用相似比得t值;
(3)PB=16-2t,BQ=11-t,分类讨论:当BP=BQ,则16-2t=11-t,解方程得t=5;当PB=PQ,作PM⊥BC于M,根据等腰三角形的性质得则BM=
BQ=
(11-t),再证明△BPM∽△BAC,利用相似比得t值.
(2)分类讨论:当3<t≤5,点Q在D点,BP=16-2t,若PD⊥BC得到△BPQ∽△BAC,利用相似比得t值;当5<t≤8,DQ=t-5,BQ=11-t,BP=16-2t,当∠PQB=90°时,△BPQ∽△BAC,利用相似比得t值;当∠BPQ=90°时,△BPQ∽△BAC,利用相似比得t值;
(3)PB=16-2t,BQ=11-t,分类讨论:当BP=BQ,则16-2t=11-t,解方程得t=5;当PB=PQ,作PM⊥BC于M,根据等腰三角形的性质得则BM=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)当点P运动到点A时,△BPQ的面积为18,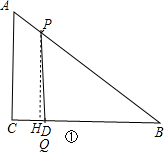
∴
•6•BD=18,解得BD=6,
∴CD=BC-BD=2,
当t=5s时,AP=2×5-6=4,点Q在D点,点P在AB上如图①,作PH⊥BC于H,
在Rt△ABC中,AC=6,BC=8,
∴AB=
=10,
∵PH∥AC,
∴△BPH∽△BAC,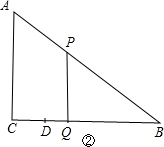
∴
=
,即
=
,解得PH=
,
∴S△PBQ=
×6×
=
,
即a=
;
故答案为:2,
;
(2)点P在边AB上,
当3<t≤5,点Q在D点,BP=16-2t,
若PD⊥BC,△BPQ∽△BAC,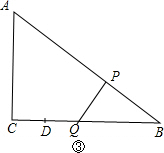
∴
=
,即
=
,解得t=
;
当5<t≤8,DQ=t-5,则BQ=8-2-(t-5)=11-t,BP=16-2t,
当∠PQB=90°时,△BPQ∽△BAC,如图②,
∵△BPQ∽△BAC,
∴
=
,即
=
,解得t=3,不合题意舍去;
当∠BPQ=90°时,△BPQ∽△BAC,如图③,
∵△BPQ∽△BCA,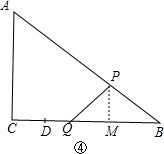
∴
=
,即
=
,解得t=6,
综上所述,当t为
或6时,△BPQ与△ABC为相似;
(3)PB=16-2t,BQ=11-t,
当BP=BQ,则16-2t=11-t,解得t=5;
当PB=PQ,作PM⊥BC于M,如图④,则BM=
BQ=
(11-t),
∵PM∥AC,
∴△BPM∽△BAC,
∴
=
,即
=
,解得t=
,
综上所述,当△BPQ是以BP为腰的等腰三角形时t的值为5或
.

∴
| 1 |
| 2 |
∴CD=BC-BD=2,
当t=5s时,AP=2×5-6=4,点Q在D点,点P在AB上如图①,作PH⊥BC于H,
在Rt△ABC中,AC=6,BC=8,
∴AB=
| AC2+BC2 |
∵PH∥AC,
∴△BPH∽△BAC,

∴
| PH |
| AC |
| BP |
| BA |
| PH |
| 6 |
| 10-4 |
| 10 |
| 18 |
| 5 |
∴S△PBQ=
| 1 |
| 2 |
| 18 |
| 5 |
| 54 |
| 5 |
即a=
| 54 |
| 5 |
故答案为:2,
| 54 |
| 5 |
(2)点P在边AB上,
当3<t≤5,点Q在D点,BP=16-2t,
若PD⊥BC,△BPQ∽△BAC,

∴
| BP |
| BA |
| BD |
| BC |
| 16-2t |
| 10 |
| 6 |
| 8 |
| 17 |
| 4 |
当5<t≤8,DQ=t-5,则BQ=8-2-(t-5)=11-t,BP=16-2t,
当∠PQB=90°时,△BPQ∽△BAC,如图②,
∵△BPQ∽△BAC,
∴
| BP |
| BA |
| BQ |
| BC |
| 16-2t |
| 10 |
| 11-t |
| 8 |
当∠BPQ=90°时,△BPQ∽△BAC,如图③,
∵△BPQ∽△BCA,

∴
| BP |
| BC |
| BQ |
| BA |
| 16-2t |
| 8 |
| 11-t |
| 10 |
综上所述,当t为
| 17 |
| 4 |
(3)PB=16-2t,BQ=11-t,
当BP=BQ,则16-2t=11-t,解得t=5;
当PB=PQ,作PM⊥BC于M,如图④,则BM=
| 1 |
| 2 |
| 1 |
| 2 |
∵PM∥AC,
∴△BPM∽△BAC,
∴
| BP |
| BA |
| BM |
| BC |
| 16-2t |
| 10 |
| ||
| 8 |
| 73 |
| 11 |
综上所述,当△BPQ是以BP为腰的等腰三角形时t的值为5或
| 73 |
| 11 |
点评:本题考查了相似的综合题:熟练掌握相似三角形的判定与性质;会从函数图象中获取信息;会根据勾股定理和相似比进行几何计算;提高运用分类讨论的思想解决数学问题的能力.

练习册系列答案
相关题目
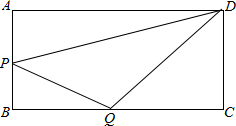 在矩形ABCD中,AB=5,BC=12,点P从点B开始沿AB向点A以1个单位每秒的速度移动,点Q从点B开始沿BC边向点C以2个单位每秒的速度移动,点P到点A或点Q到点C停止移动,如果P、Q分别从B同时出发,连接PQ、DQ、DP,问几秒钟时△DPQ的面积是8?
在矩形ABCD中,AB=5,BC=12,点P从点B开始沿AB向点A以1个单位每秒的速度移动,点Q从点B开始沿BC边向点C以2个单位每秒的速度移动,点P到点A或点Q到点C停止移动,如果P、Q分别从B同时出发,连接PQ、DQ、DP,问几秒钟时△DPQ的面积是8? 如图,Rt△ABC中,延长斜边中线CD到E,使CD=DE,连接AE,BE,则四边形AEBC是什么图形,说明理由.
如图,Rt△ABC中,延长斜边中线CD到E,使CD=DE,连接AE,BE,则四边形AEBC是什么图形,说明理由. 在△ABC中,AB=AC,∠ABC=α,点D在△ABC的内部,△BDC是等边三角形.
在△ABC中,AB=AC,∠ABC=α,点D在△ABC的内部,△BDC是等边三角形.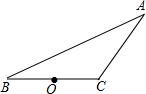 如图,已知△ABC中,O为BC的中点.
如图,已知△ABC中,O为BC的中点.