题目内容
 在△ABC中,AB=AC,∠ABC=α,点D在△ABC的内部,△BDC是等边三角形.
在△ABC中,AB=AC,∠ABC=α,点D在△ABC的内部,△BDC是等边三角形.(1)用含α的式子来表示∠ABD;
(2)求∠BDA的度数.
考点:等边三角形的性质,等腰三角形的性质
专题:
分析:(1)根据等边三角形的性质求出∠DBC度数,进而可得出结论;
(2)过点A作AE⊥BC于点E,由等腰三角形的性质可知点E为线段BC的中点,故AE是∠BDC的平分线,由平角的定义即可得出结论.
(2)过点A作AE⊥BC于点E,由等腰三角形的性质可知点E为线段BC的中点,故AE是∠BDC的平分线,由平角的定义即可得出结论.
解答: 解:(1)∵△ABC中,∠ABC=α,△BDC是等边三角形,
解:(1)∵△ABC中,∠ABC=α,△BDC是等边三角形,
∴∠ABD=∠ABC-∠DBC=α-60°;
(2)过点A作AE⊥BC于点E,
∵△ABC中,AB=AC,
∴点E为线段BC的中点,
∵△BDC是等边三角形,
∴AE是∠BDC的平分线,
∴∠BDA=180°-∠BDE=180°-30°=150°.
 解:(1)∵△ABC中,∠ABC=α,△BDC是等边三角形,
解:(1)∵△ABC中,∠ABC=α,△BDC是等边三角形,∴∠ABD=∠ABC-∠DBC=α-60°;
(2)过点A作AE⊥BC于点E,
∵△ABC中,AB=AC,
∴点E为线段BC的中点,
∵△BDC是等边三角形,
∴AE是∠BDC的平分线,
∴∠BDA=180°-∠BDE=180°-30°=150°.
点评:本题考查的是等腰三角形的性质,熟知等腰三角形“三线合一”的性质是解答此题的关键.

练习册系列答案
相关题目
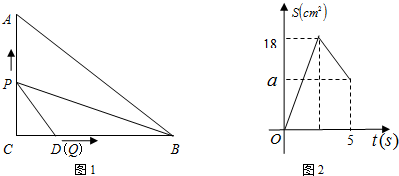
 如图,已知:在矩形ABCD中,AB=2,BC=4,P是对角线BD上的一个动点,作PF⊥BD于P,交边BC于点F(点F与B、C都不重合),E是射线FC上一动点,连接PE、ED,并一直保持∠EPF=∠FBP,设B、P两点的距离为x,△DEP的面积为y.
如图,已知:在矩形ABCD中,AB=2,BC=4,P是对角线BD上的一个动点,作PF⊥BD于P,交边BC于点F(点F与B、C都不重合),E是射线FC上一动点,连接PE、ED,并一直保持∠EPF=∠FBP,设B、P两点的距离为x,△DEP的面积为y.
 如图,已知抛物线
如图,已知抛物线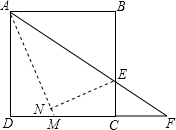 如图,正方形ABCD的边长为6,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,当AB=2CF时,求NM的长.
如图,正方形ABCD的边长为6,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,当AB=2CF时,求NM的长.