题目内容
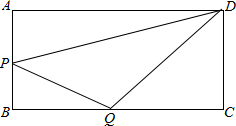 在矩形ABCD中,AB=5,BC=12,点P从点B开始沿AB向点A以1个单位每秒的速度移动,点Q从点B开始沿BC边向点C以2个单位每秒的速度移动,点P到点A或点Q到点C停止移动,如果P、Q分别从B同时出发,连接PQ、DQ、DP,问几秒钟时△DPQ的面积是8?
在矩形ABCD中,AB=5,BC=12,点P从点B开始沿AB向点A以1个单位每秒的速度移动,点Q从点B开始沿BC边向点C以2个单位每秒的速度移动,点P到点A或点Q到点C停止移动,如果P、Q分别从B同时出发,连接PQ、DQ、DP,问几秒钟时△DPQ的面积是8?考点:一元二次方程的应用
专题:几何动点问题
分析:已知了P,Q的速度,根据路程=速度×时间,可用时间表示出BP,BQ的长,然后根据三角形的面积公式,得出方程,求出未知数的值.
解答:解:设x秒后△DBQ面积为8,则PB=5-x,BQ=2x,CQ=12-x,
根据题意,得
(5-x+5)×12-
(5-x)•2x-
(12-x)×5=8
解得:x1=2,x2=4.
答:2秒或4秒后△PBQ面积为8.
根据题意,得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:x1=2,x2=4.
答:2秒或4秒后△PBQ面积为8.
点评:本题考查了一元二次方程的应用,对于面积问题应熟记各种图形的面积公式.然后根据题意列出方程,判断所求的解是否符合题意,舍去不合题意的解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知:在矩形ABCD中,AB=2,BC=4,P是对角线BD上的一个动点,作PF⊥BD于P,交边BC于点F(点F与B、C都不重合),E是射线FC上一动点,连接PE、ED,并一直保持∠EPF=∠FBP,设B、P两点的距离为x,△DEP的面积为y.
如图,已知:在矩形ABCD中,AB=2,BC=4,P是对角线BD上的一个动点,作PF⊥BD于P,交边BC于点F(点F与B、C都不重合),E是射线FC上一动点,连接PE、ED,并一直保持∠EPF=∠FBP,设B、P两点的距离为x,△DEP的面积为y. 如图,点D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.
如图,点D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.