题目内容
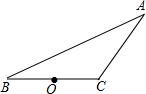 如图,已知△ABC中,O为BC的中点.
如图,已知△ABC中,O为BC的中点.(1)作出图中△ABC绕点O顺时针旋转180°后的图形△A′B′C′,请判断四边形AB′A′C′的形状,并证明你的结论;
(2)按照(1)中的方法作图,当△ABC满足什么条件时,四边形AB′A′C′是矩形、菱形或正方形?证明你的结论.
考点:作图-旋转变换
专题:
分析:(1)连接AO并延长至A′,使A′O=AO,点B的对称点B′与点C重合,点C的对称点C′与点B重合,然后顺次连接即可;再根据对角线互相平分的四边形是平行四边形证明;
(2)根据矩形、菱形、正方形的定义以及判定方法解答并证明.
(2)根据矩形、菱形、正方形的定义以及判定方法解答并证明.
解答: 解:(1)△A′B′C′如图所示,
解:(1)△A′B′C′如图所示,
∵O为BC的中点,
∴BO=CO,
又∵A′O=AO,
∴四边形AB′A′C′是平行四边形;
(2)当∠A=90°时,四边形AB′A′C′是矩形,
AB=AC时,四边形AB′A′C′是菱形,
∠A=90°且AB=AC时,四边形AB′A′C′是正方形.
证明如下:∵∠A=90°,
∴∠A′=90°,
又∵∠AB′A′=∠AC′A′,
∴∠AB′A′=∠AC′A′=
×180°=90°,
∴?AB′A′C′是矩形;
∵AB=AC,点O是BC的中点,
∴AA′⊥B′C′,
∴?AB′A′C′是菱形,
由上证明可知,∠A=90°时,?AB′A′C′是矩形,
AB=AC时,?AB′A′C′是菱形,
∴∠A=90°且AB=AC时,?AB′A′C′既是矩形也是菱形,
即,四边形AB′A′C′是正方形.
 解:(1)△A′B′C′如图所示,
解:(1)△A′B′C′如图所示,∵O为BC的中点,
∴BO=CO,
又∵A′O=AO,
∴四边形AB′A′C′是平行四边形;
(2)当∠A=90°时,四边形AB′A′C′是矩形,
AB=AC时,四边形AB′A′C′是菱形,
∠A=90°且AB=AC时,四边形AB′A′C′是正方形.
证明如下:∵∠A=90°,
∴∠A′=90°,
又∵∠AB′A′=∠AC′A′,
∴∠AB′A′=∠AC′A′=
| 1 |
| 2 |
∴?AB′A′C′是矩形;
∵AB=AC,点O是BC的中点,
∴AA′⊥B′C′,
∴?AB′A′C′是菱形,
由上证明可知,∠A=90°时,?AB′A′C′是矩形,
AB=AC时,?AB′A′C′是菱形,
∴∠A=90°且AB=AC时,?AB′A′C′既是矩形也是菱形,
即,四边形AB′A′C′是正方形.
点评:本题考查了利用旋转变换作图,主要利用了旋转变换的性质,矩形,菱形,正方形的判定,熟练掌握各图形的定义是解题的关键.

练习册系列答案
相关题目
下列方程组中,二元一次方程组是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 如图,点D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.
如图,点D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.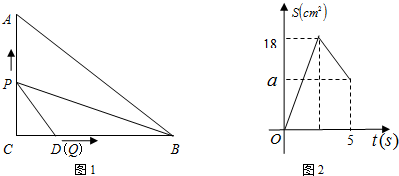
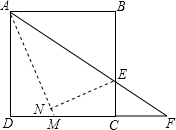 如图,正方形ABCD的边长为6,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,当AB=2CF时,求NM的长.
如图,正方形ABCD的边长为6,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,当AB=2CF时,求NM的长.