题目内容
4.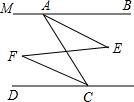 如图,已知AB∥CD,∠MAC=100°.
如图,已知AB∥CD,∠MAC=100°.(1)求∠ACD的度数;
(2)若AF平分∠BAC,CF平分∠DCA,试说明∠E=∠F的理由.完成下面的解答过程:
解:(1)∵AB∥CD(已知)
∴∠ACD+∠MAC=180°,(两直线平行同旁内角互补)
∴∠ACD=80°(角度的计算)
(2)∵AB∥CD,(已知)
∴∠BAC=∠ACD,(两直线平行内错角相等)
∵AE平分∠BAC,CF平分∠DCA,(已知)
∴∠CAE=$\frac{1}{2}$∠BAC,∠ACF=$\frac{1}{2}$∠ACD,(角平分线的定义)
∴∠CAE=∠ACF.(等式的性质)
∴AE∥CF.(内错角相等两直线平行)
∴∠E=∠F.(两直线平行内错角相等)
分析 (1)根据两直线平行同旁内角互补,即可∠ACD的度数;
(2)先根据两直线平行内错角相等,可得∠BAC=∠ACD,然后根据角平分线的定义可得∠EAC=∠FCA,然后根据内错角相等两直线平行,可得AE∥CF,进而根据两直线平行内错角相等即可证明∠E=∠F.
解答 解:(1)∵AB∥CD(已知)
∴∠ACD+∠MAC=180°,(两直线平行同旁内角互补)
∴∠ACD=80°(角度的计算)
(2)∵AB∥CD,(已知)
∴∠BAC=∠ACD,(两直线平行内错角相等)
∵AE平分∠BAC,CF平分∠DCA,(已知)
∴∠CAE=$\frac{1}{2}$∠BAC,∠ACF=$\frac{1}{2}$∠ACD,(角平分的定义)
∴∠CAE=∠ACF.(等式的性质)
∴AE∥CF.(内错角相等两直线平行)
∴∠E=∠F.(两直线平行内错角相等).
故答案为:MAC;两直线平行同旁内角互补;80°;两直线平行内错角相等;已知;角平分线的定义;CAE;ACF;内错角相等两直线平行;两直线平行内错角相等.
点评 此题考查了平行线的判定与性质,解题的关键是:熟记同位角相等?两直线平行;内错角相等?两直线平行;同旁内角互补?两直线平行.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
14.已知两圆外切,圆心距为20cm,若其中一个圆的半径是15cm,则另一个圆的半径是( )
| A. | 5cm | B. | 4cm | C. | 3cm | D. | 2cm |
19.在平面直角坐标系中有一点A(4,-2),将坐标系平移,使原点O移至点A,则在新坐标系中原来点O的坐标是( )
| A. | (-4,2) | B. | (-4,-2) | C. | (4,2) | D. | (2,-4) |
16.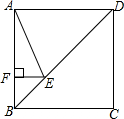 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )| A. | 4-2$\sqrt{2}$ | B. | 3$\sqrt{2}$-4 | C. | 1 | D. | $\sqrt{2}$ |
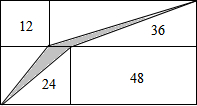 如图,大长方形由四个面积分别为12cm2、36cm2、24cm2、48cm2的小长方形拼成,求图中阴影部分的面积是多少cm2?
如图,大长方形由四个面积分别为12cm2、36cm2、24cm2、48cm2的小长方形拼成,求图中阴影部分的面积是多少cm2? 将正整数按如图所示的规律排列下去,若有序实数对(4,3)表示实数9,则表示的实数是58的有序实数对为(11,3).
将正整数按如图所示的规律排列下去,若有序实数对(4,3)表示实数9,则表示的实数是58的有序实数对为(11,3).