题目内容
9. 将正整数按如图所示的规律排列下去,若有序实数对(4,3)表示实数9,则表示的实数是58的有序实数对为(11,3).
将正整数按如图所示的规律排列下去,若有序实数对(4,3)表示实数9,则表示的实数是58的有序实数对为(11,3).
分析 根据排列规律可知从1开始,第1排1个数;第2排2个数;第3排3个数;第4排4个数…,由此得出第n排有n个数,根据此规律估算58的位置即可得出结论.
解答 解:从第1排到第n排,共有1+2+3+4+…+n=$\frac{1}{2}$n(n+1)个数,
∵$\frac{1}{2}$×10×(10+1)=55,55+3=58,
∴58在第11排第3个,表示的有序数对是(11,3).
故答案为:(11,3)
点评 此题考查数字的变化规律,解答此类题目的关键是根据题目中给出的图形、数值、数列等已知条件,认真分析,找出规律,利用规律解决问题.

练习册系列答案
相关题目
17.比较$\sqrt{7}$-1与$\frac{\sqrt{7}}{2}$的大小,结果是( )
| A. | 后者大 | B. | 前者大 | C. | 一样大 | D. | 无法确定 |
14.在平行四边形ABCD 中,∠A:∠B:∠C:∠D的值可以是( )
| A. | 1:2:1:2 | B. | 1:2:2:1 | C. | 1:2:3:4 | D. | 1:1:2:2 |
1. 如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,如果顾客乘地铁从点B到点C上升的高度为5m,则电梯BC的长是( )
如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,如果顾客乘地铁从点B到点C上升的高度为5m,则电梯BC的长是( )
 如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,如果顾客乘地铁从点B到点C上升的高度为5m,则电梯BC的长是( )
如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,如果顾客乘地铁从点B到点C上升的高度为5m,则电梯BC的长是( )| A. | 5cm | B. | 5$\sqrt{3}$cm | C. | 10m | D. | $\frac{10\sqrt{3}}{3}$m |
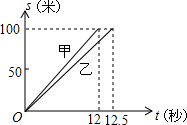 甲乙两人在一次100米赛跑中的路程s(米)和时间t(秒)的函数关系如图所示.
甲乙两人在一次100米赛跑中的路程s(米)和时间t(秒)的函数关系如图所示.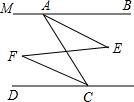 如图,已知AB∥CD,∠MAC=100°.
如图,已知AB∥CD,∠MAC=100°.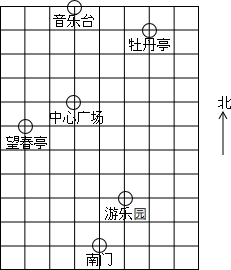 春天到了,七(1)班组织同学到人民公园春游,张明、李华对着景区示意图描述牡丹亭位置(图中小正方形边长代表100m)
春天到了,七(1)班组织同学到人民公园春游,张明、李华对着景区示意图描述牡丹亭位置(图中小正方形边长代表100m)