题目内容
16.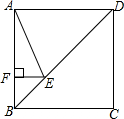 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )| A. | 4-2$\sqrt{2}$ | B. | 3$\sqrt{2}$-4 | C. | 1 | D. | $\sqrt{2}$ |
分析 根据正方形的对角线平分一组对角可得∠ABD=∠ADB=45°,再求出∠DAE的度数,根据三角形的内角和定理求∠AED,从而得到∠DAE=∠AED,再根据等角对等边的性质得到AD=DE,然后求出正方形的对角线BD,再求出BE,最后根据等腰直角三角形的直角边等于斜边的$\frac{\sqrt{2}}{2}$倍计算即可得解.
解答 解:在正方形ABCD中,∠ABD=∠ADB=45°,
∵∠BAE=22.5°,
∴∠DAE=90°-∠BAE=90°-22.5°=67.5°,
在△ADE中,∠AED=180°-45°-67.5°=67.5°,
∴∠DAE=∠AED,
∴AD=DE=4,
∵正方形的边长为4,
∴BD=4$\sqrt{2}$,
∴BE=BD-DE=4$\sqrt{2}$-4,
∵EF⊥AB,∠ABD=45°,
∴△BEF是等腰直角三角形,
∴EF=$\frac{\sqrt{2}}{2}$BE=$\frac{\sqrt{2}}{2}$×(4$\sqrt{2}$-4)=4-2$\sqrt{2}$.
故选A.
点评 本题考查了正方形的性质,主要利用了正方形的对角线平分一组对角,等角对等边的性质,正方形的对角线与边长的关系,等腰直角三角形的判定与性质,根据角的度数的相等求出相等的角,再求出DE=AD是解题的关键,也是本题的难点.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
1. 如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,如果顾客乘地铁从点B到点C上升的高度为5m,则电梯BC的长是( )
如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,如果顾客乘地铁从点B到点C上升的高度为5m,则电梯BC的长是( )
 如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,如果顾客乘地铁从点B到点C上升的高度为5m,则电梯BC的长是( )
如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,如果顾客乘地铁从点B到点C上升的高度为5m,则电梯BC的长是( )| A. | 5cm | B. | 5$\sqrt{3}$cm | C. | 10m | D. | $\frac{10\sqrt{3}}{3}$m |
8.如果$\frac{1}{3}$xa+2y3与-3x3y2b-a是同类项,那么a,b的值分别是( )
| A. | $\left\{\begin{array}{l}{a=1}\\{b=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=0}\\{b=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$ |
 如图,过?ABCD的各顶点分别作对角线的垂线AE、BF、CG、DH.垂足分别为E、F、G、H.求证:四边形EFGH是平行四边形.
如图,过?ABCD的各顶点分别作对角线的垂线AE、BF、CG、DH.垂足分别为E、F、G、H.求证:四边形EFGH是平行四边形.
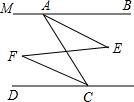 如图,已知AB∥CD,∠MAC=100°.
如图,已知AB∥CD,∠MAC=100°. 已知如图,∠1=∠2,CF⊥AB、DE⊥AB,那么∠AFG和∠B是否相等,请说明理由.
已知如图,∠1=∠2,CF⊥AB、DE⊥AB,那么∠AFG和∠B是否相等,请说明理由. 如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).