题目内容
19.在平面直角坐标系中有一点A(4,-2),将坐标系平移,使原点O移至点A,则在新坐标系中原来点O的坐标是( )| A. | (-4,2) | B. | (-4,-2) | C. | (4,2) | D. | (2,-4) |
分析 坐标系平移,原来的点相当于反向移动,根据平移中点的变化规律得出在新坐标系中原来点O的坐标是(-4,2).
解答  解:如图,在新坐标系中原来点O的坐标是(-4,2).
解:如图,在新坐标系中原来点O的坐标是(-4,2).
故选A.
点评 本题考查了坐标与图形变化-平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.作出图形更加形象直观.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
9.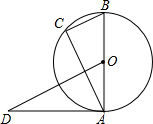 如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD,AB=2,OD=3,则BC的长为( )
如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD,AB=2,OD=3,则BC的长为( )
 如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD,AB=2,OD=3,则BC的长为( )
如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD,AB=2,OD=3,则BC的长为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
14.已知图(1)、(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB、CD交于O点,对于各图中的两个三角形而言,下列说法正确的是( )


| A. | 只有(1)相似 | B. | 只有(2)相似 | C. | 都相似 | D. | 都不相似 |
8.如果$\frac{1}{3}$xa+2y3与-3x3y2b-a是同类项,那么a,b的值分别是( )
| A. | $\left\{\begin{array}{l}{a=1}\\{b=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=0}\\{b=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$ |

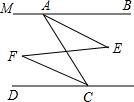 如图,已知AB∥CD,∠MAC=100°.
如图,已知AB∥CD,∠MAC=100°. 已知如图,∠1=∠2,CF⊥AB、DE⊥AB,那么∠AFG和∠B是否相等,请说明理由.
已知如图,∠1=∠2,CF⊥AB、DE⊥AB,那么∠AFG和∠B是否相等,请说明理由. 如图,P是⊙O直径CB延长线上一点,A是⊙O上一点,PA=3,PB=1,BC=8
如图,P是⊙O直径CB延长线上一点,A是⊙O上一点,PA=3,PB=1,BC=8