��Ŀ����
14�� ��ͼ��������y=$\frac{1}{4}$x2+bx+c��x�ύ�ڵ�A��-2��0������y���ڵ�B��0��-$\frac{5}{2}$����ֱ��y=kx+$\frac{3}{2}$����A��y�ύ�ڵ�C���������ߵ���һ������D
��ͼ��������y=$\frac{1}{4}$x2+bx+c��x�ύ�ڵ�A��-2��0������y���ڵ�B��0��-$\frac{5}{2}$����ֱ��y=kx+$\frac{3}{2}$����A��y�ύ�ڵ�C���������ߵ���һ������D��1����������y=$\frac{1}{4}$x2+bx+c��ֱ��y=kx+$\frac{3}{2}$�Ľ���ʽ��
��2���ٵ�P����������A��D���һ�����㣬��P����PM��y�ύ�߶�AD��M�㣬��D����DE��y���ڵ�E�����Ƿ����P��ʹ���ı���PMECΪƽ���ı��Σ������ڣ��������P�����ꣻ�������ڣ���˵������
����PN��AD�ڵ�N�����PMN���ܳ�Ϊm����P�ĺ�����Ϊt����m��t�ĺ�����ϵʽ�������m�����ֵ��
���� ��1����A��B������������y=$\frac{1}{4}$x2+bx+c�����b��c���Ӷ��õ������߽���ʽ����A���������y=kx+$\frac{3}{2}$�����k��ֵ���Ӷ��õ�һ�κ�������ʽ��
��2���Ƚⷽ����$\left\{\begin{array}{l}{y=\frac{1}{4}{x}^{2}-\frac{3}{4}x-\frac{5}{2}}\\{y=\frac{3}{4}x+\frac{3}{2}}\end{array}\right.$��D��8��$\frac{15}{2}$������ȷ��C��0��$\frac{3}{2}$������CE=6���裨x��$\frac{1}{4}$x2-$\frac{3}{4}$x-$\frac{5}{2}$������M��x��$\frac{3}{4}x$+$\frac{3}{2}$������ɱ�ʾ��MN=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4������ƽ���ı��ε��ж���������PM=CEʱ���ı���PMECΪƽ���ı��Σ���-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=6��Ȼ��ⷽ�̼��ɵõ�P�����ꣻ
��3�������ù��ɶ��������CD=10���裨t��$\frac{1}{4}$t2-$\frac{3}{4}$t-$\frac{5}{2}$������M��t��$\frac{3}{4}$t+$\frac{3}{2}$�������ʾ��MN=-$\frac{1}{4}$t2+$\frac{3}{2}$t+4����֤��Rt��PMN��Rt��DCE���������Ʊȿɵõ�MN=$\frac{3}{5}$��-$\frac{1}{4}$t2+$\frac{3}{2}$t+4����PN=$\frac{4}{5}$��-$\frac{1}{4}$t2+$\frac{3}{2}$t+4����
����m=$\frac{12}{5}$��-$\frac{1}{4}$t2+$\frac{3}{2}$t+4����Ȼ����ݶ��κ�����������⣮
��� �⣺��1����A��-2��0����B��0��-$\frac{5}{2}$������y=$\frac{1}{4}$x2+bx+c��$\left\{\begin{array}{l}{1-2b+c=0}\\{c=-\frac{5}{2}}\end{array}\right.$�����$\left\{\begin{array}{l}{b=-\frac{3}{4}}\\{c=-\frac{5}{2}}\end{array}\right.$��
���������߽���ʽΪy=$\frac{1}{4}$x2-$\frac{3}{4}$x-$\frac{5}{2}$��
��A��-2��0������y=kx+$\frac{3}{2}$��-2k+$\frac{3}{2}$=0�����k=$\frac{3}{4}$��
����һ�κ�������ʽΪy=$\frac{3}{4}$x+$\frac{3}{2}$��
��2�����ڣ�
�ⷽ����$\left\{\begin{array}{l}{y=\frac{1}{4}{x}^{2}-\frac{3}{4}x-\frac{5}{2}}\\{y=\frac{3}{4}x+\frac{3}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=8}\\{y=\frac{15}{2}}\end{array}\right.$����D��8��$\frac{15}{2}$����
��x=0ʱ��y=$\frac{3}{4}$x+$\frac{3}{2}$=+$\frac{3}{2}$����C��0��$\frac{3}{2}$����
��DE��y�ᣬ
��E��0��$\frac{15}{2}$����
��CE=OE-OC=6��
�裨x��$\frac{1}{4}$x2-$\frac{3}{4}$x-$\frac{5}{2}$������M��x��$\frac{3}{4}x$+$\frac{3}{2}$����
��MN=$\frac{3}{4}x$+$\frac{3}{2}$-��$\frac{1}{4}$x2-$\frac{3}{4}$x-$\frac{5}{2}$��=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4��
��CE��PM��
�൱PM=CEʱ���ı���PMECΪƽ���ı��Σ�
��-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=6�����x1=2��x2=4��
���ʱP������Ϊ��2��-3������4��-$\frac{3}{2}$����
��3����Rt��CDE����CE=6��DE=8��
��CD=10��
�裨t��$\frac{1}{4}$t2-$\frac{3}{4}$t-$\frac{5}{2}$������M��t��$\frac{3}{4}$t+$\frac{3}{2}$����
��MN=$\frac{3}{4}$t+$\frac{3}{2}$-��$\frac{1}{4}$t2-$\frac{3}{4}$t-$\frac{5}{2}$��=-$\frac{1}{4}$t2+$\frac{3}{2}$t+4��
��PM��CE��
���ECD=��PMN��
��Rt��PMN��Rt��DCE��
��$\frac{PM}{CD}$=$\frac{MN}{CE}$=$\frac{PN}{DE}$��
��MN=$\frac{3}{5}$��-$\frac{1}{4}$t2+$\frac{3}{2}$t+4����PN=$\frac{4}{5}$��-$\frac{1}{4}$t2+$\frac{3}{2}$t+4����
��m=PM+MN+PN=$\frac{12}{5}$��-$\frac{1}{4}$t2+$\frac{3}{2}$t+4��=-$\frac{3}{5}$��t-3��2+15��
��t=3ʱ��m�����ֵ�����ֵΪ15��
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ���������������κ��������ʺ�ƽ���ı��ε��ж��������ô���ϵ������������ʽ�������ù��ɶ��������Ʊȼ����߶εij�������������ͼ�ε����ʣ�

 ��У����ϵ�д�
��У����ϵ�д�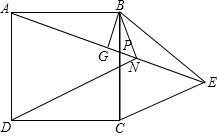 ��ͼ��PΪ������ABCD��BC����һ�㣬BG��AP�ڵ�G���ڵ�AP�ӳ�����ȡ��E��ʹAG=GE������BE��CE��
��ͼ��PΪ������ABCD��BC����һ�㣬BG��AP�ڵ�G���ڵ�AP�ӳ�����ȡ��E��ʹAG=GE������BE��CE��