题目内容
6.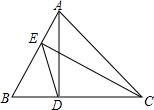 如图,在△ABC中,AD⊥BC于D,CE⊥AB于E,△ABC的面积是△BDE面积的4倍,AC=6,求DE的长.
如图,在△ABC中,AD⊥BC于D,CE⊥AB于E,△ABC的面积是△BDE面积的4倍,AC=6,求DE的长.
分析 根据有两对角相等的两个三角形相似可证明△ABD∽△CEB,有相似的性质可得BD:AB=BE:BC,再由∠B=∠B,又可以证明△BDE∽△BAC,再根据相似三角形的性质面积比等于相似比的平方即可求出DE的长.
解答 解:∵AD⊥BC于D,CE⊥AB于E,
∴∠CEB=∠ABD=90°,
∵∠B=∠B,
∴△ABD∽△CEB,
∴BD:AB=BE:BC,
又∵∠B=∠B,
∴△BDE∽△BAC,
∵△ABC的面积是△BDE面积的4倍,
∴AC:DE=2:1,
∵AC=6,
∴DE=$\frac{1}{2}$AC=3.
点评 此题考查了相似三角形的判定与性质,此题难度适中,注意掌握数形结合思想的应用,注意相似三角形的面积比是相似比的平方是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.现要把228吨物资从某地运往甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如表:
(1)求这两种货车各多少辆?
(2)如果各安排9辆货车前往甲、乙两地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为W元,求出W与a的函数关系式.(写出自变量取值范围)
| 运往地 车型 | 甲 地(元/辆) | 乙 地(元/辆) |
| 大货车 | 700 | 600 |
| 小货车 | 500 | 450 |
(2)如果各安排9辆货车前往甲、乙两地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为W元,求出W与a的函数关系式.(写出自变量取值范围)
16.某企业招聘员工,要求所要应聘者都要经过笔试与面试两种考核,且按考核总成绩从高到低进行录取,如果考核总成绩相同时,则优先录取面试成绩高分者.下面是招聘考和总成绩的计算说明:
笔试总成绩=(笔试总成绩+加分)÷2
考和总成绩=笔试总成绩+面试总成绩
现有甲、乙两名应聘者,他们的成绩情况如下:
(1)甲、乙两人面试的平均成绩为85.35,;
(2)甲应聘者的考核总成绩为145.6;
(3)根据上表的数据,若只应聘1人,则应录取甲.
笔试总成绩=(笔试总成绩+加分)÷2
考和总成绩=笔试总成绩+面试总成绩
现有甲、乙两名应聘者,他们的成绩情况如下:
| 应聘者 | 成绩 | ||
| 笔试成绩 | 加分 | 面试成绩 | |
| 甲 | 117 | 3 | 85.6 |
| 乙 | 121 | 0 | 85.1 |
(2)甲应聘者的考核总成绩为145.6;
(3)根据上表的数据,若只应聘1人,则应录取甲.
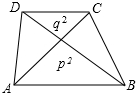 如图,梯形ABCD的两条对角线与两底所围成的两个三角形的面积分别为p2、q2,则梯形的面积为(p+q)2.
如图,梯形ABCD的两条对角线与两底所围成的两个三角形的面积分别为p2、q2,则梯形的面积为(p+q)2.