题目内容
12．把ax2-4ay2分解因式正确的是（ ）| A． | a（x+2y）（x-2y） | B． | a（x-2y）2 | C． | a（x-4y）2 | D． | a（x+4y）（x-4y） |
分析 原式提取a，再利用平方差公式分解即可．
解答 解：原式=a（x2-4y2）=a（x+2y）（x-2y），
故选A
点评 此题考查了提公式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
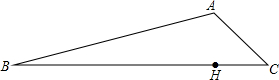2015年4月25日，尼泊尔发生8.1级地震，已知A地在这次地震中受灾严重．现有甲、乙两个小分队分别同时从B，C两地出发前往A地救援，甲沿线路BA行进，乙沿线路CA行进，已知C在A的南偏东55°方向，AB的坡度为1：5，同时由于地震原因造成BC路段泥石堵塞，在BC路段中位于A的正南方向上有一清障处H，负责清除BC路障，已知BH为12000m．
20．对于任意非零实数a、b，定义运算“⊕”，使下列式子成立：1⊕2=-$\frac{3}{2}$，2⊕1=$\frac{3}{2}$，（-2）⊕5=$\frac{21}{10}$，5⊕（-2）=-$\frac{21}{10}$，…，则（-3）⊕（-4）=（ ）
| A． | -$\frac{7}{12}$ | B． | $\frac{7}{12}$ | C． | -$\frac{25}{12}$ | D． | $\frac{25}{12}$ |
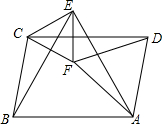如图所示，在平行四边形ABCD中，分别以AB、AD为边作等边△ABE和等边△ADF，分别连接CE、CF和EF，则下列结论中一定成立的是①②③（把所有正确结论的序号都填在横线上）．
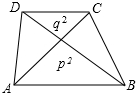如图，梯形ABCD的两条对角线与两底所围成的两个三角形的面积分别为p2、q2，则梯形的面积为（p+q）2．
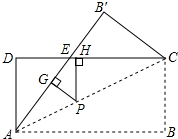如图，将矩形纸片ABCD沿对角线AC折叠，使点B落到点B′的位置，AB′与CD交于点E．