题目内容
5.某电子产品经过11月、12月连续两次降价,售价由3900元降到了2500元.设平均每月降价的百分率为x,根据题意列出的方程是( )| A. | 3900(1+x)2=2500 | B. | 3900(1-x)2=2500 | C. | 3900(1-2x)=2500 | D. | 2500(1+x)2=3900 |
分析 可根据:原售价×(1-降价的百分率)2=降低后的售价得出两次降价后的价格,然后即可列出方程.
解答 解:设平均每月降价的百分率为x,依题意得:
3900(1-x)2=2500,
故选B.
点评 本题考查由实际问题抽象出一元二次方程中求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.

练习册系列答案
相关题目
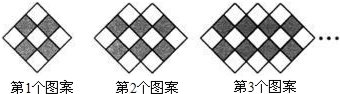
15.如图,正四边形有2条对角线,正五边形有5条对角线,正六边形有9条对角线,则正十边形有( )条对角线.


| A. | 27 | B. | 35 | C. | 40 | D. | 44 |
20.对于任意非零实数a、b,定义运算“⊕”,使下列式子成立:1⊕2=-$\frac{3}{2}$,2⊕1=$\frac{3}{2}$,(-2)⊕5=$\frac{21}{10}$,5⊕(-2)=-$\frac{21}{10}$,…,则(-3)⊕(-4)=( )
| A. | -$\frac{7}{12}$ | B. | $\frac{7}{12}$ | C. | -$\frac{25}{12}$ | D. | $\frac{25}{12}$ |
15.现要把228吨物资从某地运往甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如表:
(1)求这两种货车各多少辆?
(2)如果各安排9辆货车前往甲、乙两地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为W元,求出W与a的函数关系式.(写出自变量取值范围)
| 运往地 车型 | 甲 地(元/辆) | 乙 地(元/辆) |
| 大货车 | 700 | 600 |
| 小货车 | 500 | 450 |
(2)如果各安排9辆货车前往甲、乙两地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为W元,求出W与a的函数关系式.(写出自变量取值范围)
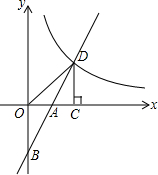 如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A.B两点,与双曲线y=$\frac{k}{x}$(x>0)交于点D,过点D作DC⊥x轴,垂足为C,且点A是OC的中点,连接OD,
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A.B两点,与双曲线y=$\frac{k}{x}$(x>0)交于点D,过点D作DC⊥x轴,垂足为C,且点A是OC的中点,连接OD,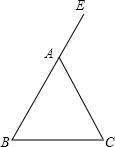 如图,在△ABC中,AB=AC=10cm,BC=12cm,E是BA延长线的一点.
如图,在△ABC中,AB=AC=10cm,BC=12cm,E是BA延长线的一点.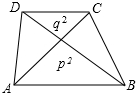 如图,梯形ABCD的两条对角线与两底所围成的两个三角形的面积分别为p2、q2,则梯形的面积为(p+q)2.
如图,梯形ABCD的两条对角线与两底所围成的两个三角形的面积分别为p2、q2,则梯形的面积为(p+q)2.