题目内容
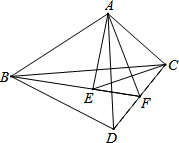 如图,△ABC,分别以AB、AC为边作等边三角形ABD与等边三角形ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论:①BE=CD;②FA平分∠EFC;③FE=FD;④FE+FC=FA;其中一定正确的结论有( )个.
如图,△ABC,分别以AB、AC为边作等边三角形ABD与等边三角形ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论:①BE=CD;②FA平分∠EFC;③FE=FD;④FE+FC=FA;其中一定正确的结论有( )个.| A、1 | B、2 | C、3 | D、4 |
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:先在AF上找到点G使得FG=EF,证出△BAE≌△DAC,可得BE=CD,从而得出①正确;先证出A、E、F、C四点共圆,根据AE=AC,可得FA平分∠EFC,从而得出②正确;根据CF+EF=AF,CF+DF=CD,得出CD≠AF,从而得出FE≠FD,即可得出③错误;根据全等三角形的判定与性质得出△AGE≌△CFE,可得AG=CF,即可求得AF=CF+EF,从而得出④正确;
解答:解:在AF上找到点G使得FG=EF,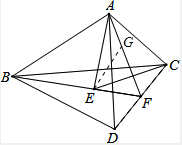
∵∠BAE+∠DAE=60°,∠CAD+∠DAE=60°,
∴∠BAE=∠DAC,
在△BAE和△DAC中,
,
∴△BAE≌△DAC,(SAS)
∴BE=CD,①正确;
∠BEA=∠ACD,
∵∠AEB+∠AEF=180°,
∴∠AEF+∠ACF=180°,
∴A、E、F、C四点共圆,
∴∠EFC=120°,
∵AE=AC,
∴∠AFC=∠AFE,即FA平分∠EFC,②正确;
∵FG=EF,∠AFE=60°,
∴△EFG是等边三角形,
∴EF=EG,
∵∠AEG+∠CEG=60°,∠CEG+∠CEF=60°,
∴∠AEG=∠CEF,
在△AGE和△CFE中,
,
∴△AGE≌△CFE(SAS),
∴AG=CF,
∵AF=AG+FG,
∴AF=CF+EF,④正确;
∵CF+EF=AF,CF+DF=CD,
CD≠AF,
∴FE=FD,③错误,
∴正确的结论有3个.
故选C.

∵∠BAE+∠DAE=60°,∠CAD+∠DAE=60°,
∴∠BAE=∠DAC,
在△BAE和△DAC中,
|
∴△BAE≌△DAC,(SAS)
∴BE=CD,①正确;
∠BEA=∠ACD,
∵∠AEB+∠AEF=180°,
∴∠AEF+∠ACF=180°,
∴A、E、F、C四点共圆,
∴∠EFC=120°,
∵AE=AC,
∴∠AFC=∠AFE,即FA平分∠EFC,②正确;
∵FG=EF,∠AFE=60°,
∴△EFG是等边三角形,
∴EF=EG,
∵∠AEG+∠CEG=60°,∠CEG+∠CEF=60°,
∴∠AEG=∠CEF,
在△AGE和△CFE中,
|
∴△AGE≌△CFE(SAS),
∴AG=CF,
∵AF=AG+FG,
∴AF=CF+EF,④正确;
∵CF+EF=AF,CF+DF=CD,
CD≠AF,
∴FE=FD,③错误,
∴正确的结论有3个.
故选C.
点评:本题考查了全等三角形的判定、全等三角形对应边相等的性质和圆周角原理,证出△BAE≌△DAC和△AGE≌△CFE是解决本题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
2014年某公司购进耗材约2015000000元,2015000000元用科学记数法表示为( )
| A、2.015×109元 |
| B、2.015×107元 |
| C、2.015×1011元 |
| D、2.015×106元 |
 如图,在平行四边形ABCD中,E是AB延长线上的一点,DE交BC于点F.已知
如图,在平行四边形ABCD中,E是AB延长线上的一点,DE交BC于点F.已知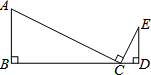 如图,在△ABC和△CDE中,∠B=∠D=90°,C为线段BD上一点,且AC⊥CE.AB=3,DE=2,BC=6.求CD的长.
如图,在△ABC和△CDE中,∠B=∠D=90°,C为线段BD上一点,且AC⊥CE.AB=3,DE=2,BC=6.求CD的长.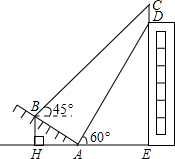 如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1:
如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1: