题目内容
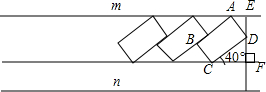 某住宅小区的物业管理部门为解决部门为解决住户停车困难问题,将一条道路开辟为停车场,停车位置如图所示,已知矩形ABCD是供一辆机动车停放的车位,其中AB=5.4m,BC=2.2m,∠DCF=40°.请计算停车位所占道路的宽度EF.(结果精确到0.1m)参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84.
某住宅小区的物业管理部门为解决部门为解决住户停车困难问题,将一条道路开辟为停车场,停车位置如图所示,已知矩形ABCD是供一辆机动车停放的车位,其中AB=5.4m,BC=2.2m,∠DCF=40°.请计算停车位所占道路的宽度EF.(结果精确到0.1m)参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84.| A、8.6 | B、5.2 |
| C、4.8 | D、5.6 |
考点:解直角三角形的应用
专题:
分析:在直角三角形中,利用三角函数关系,由已知角度和边求得ED和DF,而求得EF的长.
解答:解:由题意知∠DFC=90°,∠DEA=90°∠DCF=40°,
又∵ABCD是矩形,
∴AB=CD=5.4米,BC=AD=2.2米,∠ADC=90°,
∵∠DCF+∠CDF=90°,∠ADE+∠CDF=90°,
∴∠DCF=∠ADE=40°,
在Rt△DCF中,sin∠DCF=
,
DF=CDsin∠DCF=5.4×sin40°≈5.4×0.64=3.456,
在Rt△DAE中,COS∠ADE=
,
DE=ADcos∠ADE=2.2×cos40°≈2.2×0.77=1.694,
EF=DE+DF≈3.456+1.694=5.2,
∴停车位所占道路宽度EF约为5.2米.
故选B.
又∵ABCD是矩形,
∴AB=CD=5.4米,BC=AD=2.2米,∠ADC=90°,
∵∠DCF+∠CDF=90°,∠ADE+∠CDF=90°,
∴∠DCF=∠ADE=40°,
在Rt△DCF中,sin∠DCF=
| DF |
| CD |
DF=CDsin∠DCF=5.4×sin40°≈5.4×0.64=3.456,
在Rt△DAE中,COS∠ADE=
| DE |
| AD |
DE=ADcos∠ADE=2.2×cos40°≈2.2×0.77=1.694,
EF=DE+DF≈3.456+1.694=5.2,
∴停车位所占道路宽度EF约为5.2米.
故选B.
点评:本题考查三角函数关系的利用,结合实际问题并灵活利用正弦和余弦函数而求得.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 把两个全等的矩形ABCD和矩形CEFG拼成如图所示的图案,若BC=4,AB=2,则△ACF的面积为
把两个全等的矩形ABCD和矩形CEFG拼成如图所示的图案,若BC=4,AB=2,则△ACF的面积为 如图,△ABC为等边三角形,边长为4,F为BC边上一个动点(不与B,C重合),DF⊥AB,EF⊥AC,垂足分别为D和E.
如图,△ABC为等边三角形,边长为4,F为BC边上一个动点(不与B,C重合),DF⊥AB,EF⊥AC,垂足分别为D和E.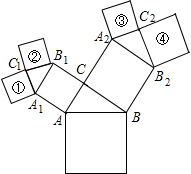 如图是我们熟悉的“勾股树”,图中的三角形都是直角三角形,四边形都是正方形,其中∠ACB=∠A1C1B1=∠A2C2B2=90°,正方形①和②的面积比、正方形③和④的面积比均为1:2.
如图是我们熟悉的“勾股树”,图中的三角形都是直角三角形,四边形都是正方形,其中∠ACB=∠A1C1B1=∠A2C2B2=90°,正方形①和②的面积比、正方形③和④的面积比均为1:2.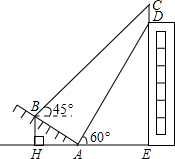 如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1:
如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1: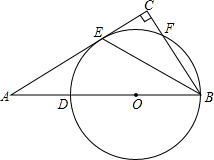 如图,Rt△ABC中,∠C=90°,D在AB上,BE平分∠ABC交AC于点E,以BD为直径的圆经过点E,交BC于点F.
如图,Rt△ABC中,∠C=90°,D在AB上,BE平分∠ABC交AC于点E,以BD为直径的圆经过点E,交BC于点F.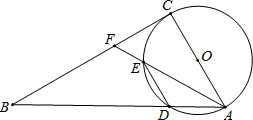 如图,以Rt△ABC的边AC为直径的⊙O交斜边AB于点D,点F为BC上一点,AF交⊙O于点E,且DE∥AC.
如图,以Rt△ABC的边AC为直径的⊙O交斜边AB于点D,点F为BC上一点,AF交⊙O于点E,且DE∥AC.