题目内容
14.已知等边△ABC中,A(-1,0),B(5,0),则点C的坐标为( )| A. | (2,3$\sqrt{3}$) | B. | (2,-3$\sqrt{3}$) | C. | (3$\sqrt{3}$,2) | D. | (2,3$\sqrt{3}$)或(2,-3$\sqrt{3}$) |
分析 作CH⊥AB于H.根据点A和B的坐标,得AB=6.根据等腰三角形的三线合一的性质,得AH=BH=3,再根据勾股定理求得CH=3$\sqrt{3}$,从而写出点C的坐标.
解答 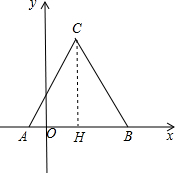 解:如图,作CH⊥AB于H.
解:如图,作CH⊥AB于H.
∵A(-1,0),B(5,0),
∴AB=6.
∵△ABC是等边三角形,
∴AH=BH=3.
根据勾股定理,得CH=3$\sqrt{3}$.
∴C(2,3$\sqrt{3}$);
同理,当点C在第四象限时,C(2,-3$\sqrt{3}$).
∴C点坐标为:C(2,3$\sqrt{3}$)或(2,-3$\sqrt{3}$);
故选D.
点评 此题综合运用了等边三角形的性质、勾股定理、坐标与图形的性质,关键是根据题意画出图形,不要漏解.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
13.一个五次单项式的系数为1,且同时含有字母a、b、c,那么这样的单项式有( )
| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
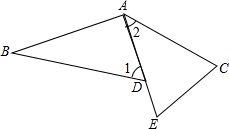 如图,∠BAC=120°,AB=AC,∠1=∠E=60°.求证:
如图,∠BAC=120°,AB=AC,∠1=∠E=60°.求证: