题目内容
19.将三张质地相同并分别标有数字1、2、3的卡片,背面朝上放在桌面上,洗匀后,甲同学从中随机抽取一张卡片.(1)甲同学抽到卡片上的数恰好是方程x2-4x+3=0的根的概率为$\frac{2}{3}$;
(2)甲乙两人约定:甲先随机抽取一张卡片后,背面朝上放回桌面洗匀,然后乙再随机抽取一张卡片,若两人所抽取卡片上的数字恰好是方程x2-4x+3=0的两个根,则甲获胜;否则乙获胜.请你通过列表或画树状图的方法,说明这个游戏是否公平?
分析 (1)解方程求出方程的根,即可求出甲同学抽到卡片上的数恰好是方程x2-4x+3=0的根的概率;
(2)列表或画树形图,然后根据概率公式计算出甲获胜和乙获胜的概率,再利用概率的大小来判断游戏是否公平.
解答 解:(1)∵x2-4x+3=0,
∴x=1或3,
∴甲同学抽到卡片上的数恰好是方程x2-4x+3=0的根的概率=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$;
(2)列表如下:
| 1 | 2 | 3 | |
| 1 | (1,1) | (1,2) | (1,3) |
| 2 | (2,1) | (2,2) | (2,3) |
| 3 | (3,1) | (3,2) | (3,3) |
∵P(甲获胜)=$\frac{2}{9}$,P(乙获胜)=$\frac{7}{9}$,
∴P(甲获胜)<P(乙获胜),
∴游戏不公平.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9. 如图,在△ABC中,AB=5,AC=12,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )
如图,在△ABC中,AB=5,AC=12,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )
 如图,在△ABC中,AB=5,AC=12,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )
如图,在△ABC中,AB=5,AC=12,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为( )| A. | 10 | B. | 12 | C. | 13 | D. | 17 |
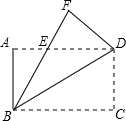 如图,把矩形ABCD沿对角线BD折叠使点C落在F处,BF交AD于点E.
如图,把矩形ABCD沿对角线BD折叠使点C落在F处,BF交AD于点E. 解不等式组$\left\{\begin{array}{l}{3x+1≥-5①}\\{2x-1≤3②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{3x+1≥-5①}\\{2x-1≤3②}\end{array}\right.$ 如图,直线AB∥CD,BC平分∠ABD,若∠1=54°,则∠2=72°.
如图,直线AB∥CD,BC平分∠ABD,若∠1=54°,则∠2=72°.