题目内容
15．已知关于x的方程x2-2mx+m2+m-2=0有两个不相等的实数根．（1）求m的取值范围；
（2）当m为正整数时，求方程的根．
分析 （1）利用判别式的意义得到=（-2m）2-4（m2+m-2）＞0，然后解不等式即可；
（2）利用m的范围确定m的正整数值为1，则方程化为x2-2x=0，然后利用因式分解法解方程．
解答 解：（1）根据题意得△=（-2m）2-4（m2+m-2）＞0，
解得m＜2；
（2）m的正整数值为1，
方程化为x2-2x=0，
解得x1=0，x2=2．
点评 本题考查了根的判别式：一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：当△＞0时，方程有两个不相等的两个实数根；当△=0时，方程有两个相等的两个实数根；当△＜0时，方程无实数根．
练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
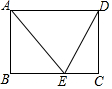如图，矩形ABCD中，AE平分∠BAD，并交BC于点E，ED=5cm，EC=3cm，则矩形的周长为22cm，面积为28cm2．
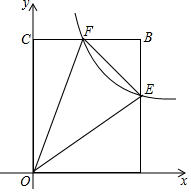如图在矩形OABC中，OA=5，OC=6，反比例函数的图象与AB、BC分别交于点E、F，且AE＜EB，△OEF与△BEF的面积之差等于5$\frac{11}{30}$，求此反比例函数的解析式．
如图，正方形ABCD中，AD为⊙O的直径，E为AB上一点将正方形沿EC折叠，点B落在⊙O上的F点．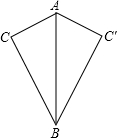
如图所示，∠C=∠C′=90°，AC=AC′，求证：∠CAB=∠C′AB（要求不用全等的知识证明）．