题目内容
11.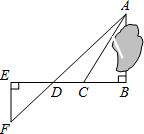 为了测量被池塘隔开的A、B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上,有四位同学分别测量出相关数据:甲为“BC、∠ACB”;乙为“CD、∠ACB”;丙为“EF、DE、BD”;丁为“DE、DC、BC”.根据所测数据,不能求出A、B间距离的是乙和丁同学.
为了测量被池塘隔开的A、B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上,有四位同学分别测量出相关数据:甲为“BC、∠ACB”;乙为“CD、∠ACB”;丙为“EF、DE、BD”;丁为“DE、DC、BC”.根据所测数据,不能求出A、B间距离的是乙和丁同学.
分析 利用三角函数由A同学测量出的数据可求出A、B间距离,而由丙测量出的数据不能求出A、B间距离;根据三角形相似的判定与性质可由丙同学测量出的数据可求出A、B间距离,而丁测量出的数据不能求出A、B间距离.
解答 解:在Rt△ABC中,tan∠ACB=$\frac{AB}{BC}$,则BC=AB•tan∠ACB,所以甲同学测量出的数据可求出A、B间距离;
∵AB∥EF,
∴△ABD∽△FED,
∴$\frac{AB}{EF}$=$\frac{BD}{DE}$,则AB=$\frac{EF•BD}{DE}$,所以丙同学测量出的数据可求出A、B间距离.
∴不能求出A、B间距离的是乙和丁同学.
故答案为乙和丁.
点评 本题考查了相似三角形的应用:借助标杆或直尺测量物体的高度.利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.也考查了解直角三角形.

练习册系列答案
相关题目
16. 如图,AB是圆O的直径,AB⊥CD于点E,若CD=8,则DE等于( )
如图,AB是圆O的直径,AB⊥CD于点E,若CD=8,则DE等于( )
 如图,AB是圆O的直径,AB⊥CD于点E,若CD=8,则DE等于( )
如图,AB是圆O的直径,AB⊥CD于点E,若CD=8,则DE等于( )| A. | 3 | B. | 5 | C. | 4 | D. | 6 |
20.把一个正方形的一边增加2cm,另一边增加1cm,得到的矩形面积的2倍比正方形的面积多11cm2.设这个正方形的边长为x cm,依题意可得方程为( )
| A. | (x+2)(x+1)=2x2+14 | B. | 2(x+2)(x+1)=x2+11 | C. | 2(x-2)(x-1)=x2+11 | D. | (x-2)(x-1)=2x2+11 |
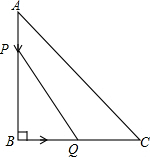 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=3cm,点P从点A开始出发沿AB向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果点P、Q分别从A、B同时出发,当P、Q到达B、C时停止运动.求:几秒中后,P、Q间的距离为4$\sqrt{2}$cm?
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=3cm,点P从点A开始出发沿AB向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果点P、Q分别从A、B同时出发,当P、Q到达B、C时停止运动.求:几秒中后,P、Q间的距离为4$\sqrt{2}$cm?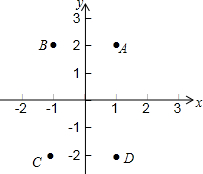 如图,平面内四个点的坐标分别为A(1,2),B(-1,2),C(-1,-2),D(1,-2),依次连接点A,B,C,D,则四边形ABCD的面积为( )
如图,平面内四个点的坐标分别为A(1,2),B(-1,2),C(-1,-2),D(1,-2),依次连接点A,B,C,D,则四边形ABCD的面积为( )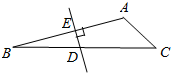 如图所示,在△ABC中,∠C=45°,∠B=15°,AB的垂直平分线交AB于E,交BC于D,DB=10,那么AC=5$\sqrt{2}$.
如图所示,在△ABC中,∠C=45°,∠B=15°,AB的垂直平分线交AB于E,交BC于D,DB=10,那么AC=5$\sqrt{2}$. 如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,点B的坐标为(3,-$\frac{3}{2}$)直线l1,l2交于点C.
如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,点B的坐标为(3,-$\frac{3}{2}$)直线l1,l2交于点C.