题目内容
6.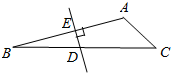 如图所示,在△ABC中,∠C=45°,∠B=15°,AB的垂直平分线交AB于E,交BC于D,DB=10,那么AC=5$\sqrt{2}$.
如图所示,在△ABC中,∠C=45°,∠B=15°,AB的垂直平分线交AB于E,交BC于D,DB=10,那么AC=5$\sqrt{2}$.
分析 由AB边的垂直平分线交AB于E,交BC于D,可得AD=BD,继而求得∠ADC=30°,然后利用含30°角的直角三角形和等腰直角三角形的性质,求得答案.
解答  解:连接AD,过A作AF⊥BC于F,
解:连接AD,过A作AF⊥BC于F,
∵DE是AB的垂直平分线,
∴AD=BD=10,
∴∠DAE=∠B=15°,
∴∠ADF=30°,
∴AF=$\frac{1}{2}$AD=5,
∵∠C=45°,
∴AC=$\sqrt{2}$AF=5$\sqrt{2}$,
故答案为:5$\sqrt{2}$.
点评 本题考查了线段的垂直平分线的性质,三角形外角的性质,等腰直角三角形的性质,熟知线段垂直平分线上的点到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
 如图所示,I为△ABC的内心,M为BC的中点,四边形IQDM为平行四边形,求证:∠QMD=90°.
如图所示,I为△ABC的内心,M为BC的中点,四边形IQDM为平行四边形,求证:∠QMD=90°.
 如图,在Rt△ABC中,∠C=90°,∠A=31°,AB=10,求BC的长.(结果精确到0.01)
如图,在Rt△ABC中,∠C=90°,∠A=31°,AB=10,求BC的长.(结果精确到0.01)
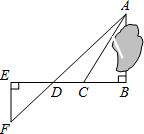 为了测量被池塘隔开的A、B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上,有四位同学分别测量出相关数据:甲为“BC、∠ACB”;乙为“CD、∠ACB”;丙为“EF、DE、BD”;丁为“DE、DC、BC”.根据所测数据,不能求出A、B间距离的是乙和丁同学.
为了测量被池塘隔开的A、B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上,有四位同学分别测量出相关数据:甲为“BC、∠ACB”;乙为“CD、∠ACB”;丙为“EF、DE、BD”;丁为“DE、DC、BC”.根据所测数据,不能求出A、B间距离的是乙和丁同学. 如图,已知∠BOD=80°,四边形ABCD的四个顶点都在圆O上,那么∠DAB的度数为140°.
如图,已知∠BOD=80°,四边形ABCD的四个顶点都在圆O上,那么∠DAB的度数为140°.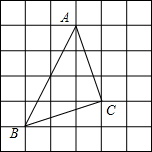 如图所示的方格纸中,每一格小正方形的边长均为1,小莉画出一个等腰直角三角形ABC,她画得对吗?请你设法验证一下,并与同伴交流各自的方法.
如图所示的方格纸中,每一格小正方形的边长均为1,小莉画出一个等腰直角三角形ABC,她画得对吗?请你设法验证一下,并与同伴交流各自的方法.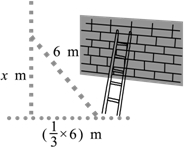 生活表明,靠墙摆放梯子时,若梯子底端离墙的距离为梯子长度的三分之一,则梯子比较稳定.现有一长度为6m的梯子,当梯子稳定摆放时,它的顶端最多能到达多高?(精确到0.1m)
生活表明,靠墙摆放梯子时,若梯子底端离墙的距离为梯子长度的三分之一,则梯子比较稳定.现有一长度为6m的梯子,当梯子稳定摆放时,它的顶端最多能到达多高?(精确到0.1m)