题目内容
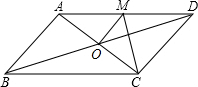如图，?ABCD的对角线相交于点O，且AD≠CD，过点O作OM⊥AO交AD于点M，若C△CDM=a，求C?ABCD．考点：平行四边形的性质
专题：
分析：由四边形ABCD是平行四边形，即可得AB=CD，AD=BC，OA=OC，又由OM⊥AC，根据垂直平分线的性质，即可得AM=CM，又由△CDM的周长是a，即可求得平行四边形ABCD的周长．
解答：解：∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC，OA=OC，
∵OM⊥AC，
∴AM=CM，
∵△CDM的周长是a，
即：DM+CM+CD=DM+AM+CD=AD+CD=a，
∴平行四边形ABCD的周长为：2（AD+CD）=2×a=2a．
∴平行四边形ABCD的周长为2a．
∴AB=CD，AD=BC，OA=OC，
∵OM⊥AC，
∴AM=CM，
∵△CDM的周长是a，
即：DM+CM+CD=DM+AM+CD=AD+CD=a，
∴平行四边形ABCD的周长为：2（AD+CD）=2×a=2a．
∴平行四边形ABCD的周长为2a．
点评：此题考查了平行四边形的性质与线段垂直平分线的性质．此题难度适中，注意掌握数形结合思想与转化思想的应用．
练习册系列答案
口算题天天练系列答案
相关题目
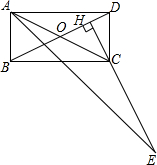如图，在矩形ABCD中，点H在对角线BD上．HC⊥BD，HC的延长线交∠BAD的平分线于点E．求证：CE=BD．
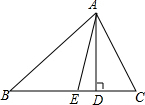如图所示，在△ABC中，已知∠C＞∠B，AD⊥BC于点D，AE平分∠BAC，判断∠EAD与
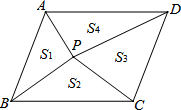如图，点P是平行四边形ABCD内的任意一点，连接PA、PB、PC、PD，得到△PAB、△PBC、△PCD、△PDA，设它们的面积分别是S1、S2、S3、S4，给出如下结论：
四边形ABCD是正方形，圆心角等于90°，OE=OF=10，问：正方形边长多少？
如图，点D是△ABC的外接圆的弧
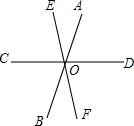如图，直线AB，CD，EF相交于点O，∠AOE：∠AOD=1：3，∠COB：∠DOF=3：4，求证，CD⊥EF．
如图，在⊙O中，OD⊥BC，∠BOD=50°，则∠CAD的度数等于（ ）| A、30° | B、25° |
| C、20° | D、15° |
如图，直线AB经过点A（0，-4），B（-1，0），与双曲线y=