题目内容
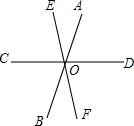 如图,直线AB,CD,EF相交于点O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4,求证,CD⊥EF.
如图,直线AB,CD,EF相交于点O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4,求证,CD⊥EF.考点:垂线,对顶角、邻补角
专题:证明题
分析:设∠AOE=x,则∠AOD=3x,得出∠COE=DOF=4x,列出方程4x+x+3x=180°,解方程即可得出结论.
解答:证明:设∠AOE=x,则∠AOD=3x,
∴∠COB=∠AOD=3x,
∴∠DOF=4x,
∵∠COE=DOF=4x,∠COE+∠AOE+∠AOD=180°,
∴4x+x+3x=180°,
∴x=22.5°,
∴∠COE=4×22.5°=90°,
∴CD⊥EF.
∴∠COB=∠AOD=3x,
∴∠DOF=4x,
∵∠COE=DOF=4x,∠COE+∠AOE+∠AOD=180°,
∴4x+x+3x=180°,
∴x=22.5°,
∴∠COE=4×22.5°=90°,
∴CD⊥EF.
点评:本题考查了垂线.对顶角、邻补角的定义;弄清各个角之间的数量关系是解决问题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 一次函数y=ax+6与y=cx-b的图象交于点P(1,b),一次函数y=ax+6的图象交y轴于点A,y=cx-b的图象交y轴于点B,如图所示.若△ABP的面积为4,则一次函数y=cx-b的图象与直线y=4和y轴所围成的阴影部分的面积为( )
一次函数y=ax+6与y=cx-b的图象交于点P(1,b),一次函数y=ax+6的图象交y轴于点A,y=cx-b的图象交y轴于点B,如图所示.若△ABP的面积为4,则一次函数y=cx-b的图象与直线y=4和y轴所围成的阴影部分的面积为( )| A、4 | B、4.5 | C、8 | D、9 |
下列四个多项式中,是x2-2x-8因式的为( )
| A、x+2 | B、x-2 |
| C、x+8 | D、x+4 |




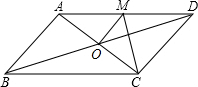 如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AO交AD于点M,若C△CDM=a,求C?ABCD.
如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AO交AD于点M,若C△CDM=a,求C?ABCD. 墙壁D处有一盏灯(如图),小明站在A处测得他的影长与身长相等都为1.5m,小明向墙壁走1m到B处发现影子刚好落在A点,则灯泡与地面的距离CD=
墙壁D处有一盏灯(如图),小明站在A处测得他的影长与身长相等都为1.5m,小明向墙壁走1m到B处发现影子刚好落在A点,则灯泡与地面的距离CD= 如图,已知:圆的两弦AB、CD相交于点P,AD、CB的延长线相交于圆外一点Q,∠AQC=36°,∠APC=80°.求∠ADC和∠BCD的度数.
如图,已知:圆的两弦AB、CD相交于点P,AD、CB的延长线相交于圆外一点Q,∠AQC=36°,∠APC=80°.求∠ADC和∠BCD的度数. 合肥市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为48m,这栋高楼有多高?(结果精确到1m,参考数据:
合肥市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为48m,这栋高楼有多高?(结果精确到1m,参考数据: