题目内容
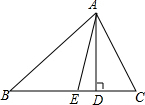 如图所示,在△ABC中,已知∠C>∠B,AD⊥BC于点D,AE平分∠BAC,判断∠EAD与
如图所示,在△ABC中,已知∠C>∠B,AD⊥BC于点D,AE平分∠BAC,判断∠EAD与| 1 |
| 2 |
考点:三角形内角和定理
专题:
分析:根据三角形内角和定理求出∠BAC=180°-(∠B+∠C),求出∠DAC和∠EAC,相减即可得出答案.
解答:解:∠EAD=
(∠C-∠B),
理由是:∠BAC=180°-(∠B+∠C),
∵AE平分∠BAC,
∴∠EAC=
∠BAC=90°-
(∠B+∠C),
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=90°-∠C,
∴∠EAD=∠EAC-∠DAC=90°-
(∠B+∠C)-(90°-∠C)=
(∠C-∠B).
| 1 |
| 2 |
理由是:∠BAC=180°-(∠B+∠C),
∵AE平分∠BAC,
∴∠EAC=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=90°-∠C,
∴∠EAD=∠EAC-∠DAC=90°-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形内角和定理,角平分线定义的应用,解此题的关键是能用∠B和∠C表示出∠EAC和∠DAC,难度适中.

练习册系列答案
相关题目
 如图,平面直角坐标系中,直线AB与x轴,y轴分别交与A(3,0)、B(0,
如图,平面直角坐标系中,直线AB与x轴,y轴分别交与A(3,0)、B(0, 一次函数y=ax+6与y=cx-b的图象交于点P(1,b),一次函数y=ax+6的图象交y轴于点A,y=cx-b的图象交y轴于点B,如图所示.若△ABP的面积为4,则一次函数y=cx-b的图象与直线y=4和y轴所围成的阴影部分的面积为( )
一次函数y=ax+6与y=cx-b的图象交于点P(1,b),一次函数y=ax+6的图象交y轴于点A,y=cx-b的图象交y轴于点B,如图所示.若△ABP的面积为4,则一次函数y=cx-b的图象与直线y=4和y轴所围成的阴影部分的面积为( ) 指出图中∠A的同位角.∠B的内错角和同旁内角.
指出图中∠A的同位角.∠B的内错角和同旁内角. 如图,直线AB,CD被EF所截,如果∠1与∠2互补,且∠1=120°,那么∠3,∠4的度数各是多少?
如图,直线AB,CD被EF所截,如果∠1与∠2互补,且∠1=120°,那么∠3,∠4的度数各是多少?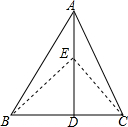 如图所示,在△ABC中,底边BC=8cm,高AD=6cm,点E为AD上一动点,当点E从点D附近向点A运动时,△BEC的面积发生了变化
如图所示,在△ABC中,底边BC=8cm,高AD=6cm,点E为AD上一动点,当点E从点D附近向点A运动时,△BEC的面积发生了变化



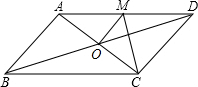 如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AO交AD于点M,若C△CDM=a,求C?ABCD.
如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AO交AD于点M,若C△CDM=a,求C?ABCD.