题目内容
15. 如图,△ABC与△A1B1C1关于直线l对称,且∠A=92°,∠C1=32°,则∠B的度数为56°.
如图,△ABC与△A1B1C1关于直线l对称,且∠A=92°,∠C1=32°,则∠B的度数为56°.
分析 根据轴对称的性质可得△ABC与△A1B1C1全等,再根据全等三角形对应角相等可得∠C=∠C1,然后利用三角形的内角和定理列式计算即可得解.
解答 解:∵△ABC与△A1B1C1关于直线l对称,
∴△ABC≌△A1B1C1,
∴∠C=∠C1=32°,
∴∠B=180°-∠A-∠C=180°-92°-32°=56°.
故答案为:56°.
点评 本题考查了轴对称的性质,全等三角形的性质,三角形的内角和定理,熟记各性质是解题的关键.

练习册系列答案
相关题目
20.若一个三角形三个内角度数的比为2:3:7,那么这个三角形是( )
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 等边三角形 |
4.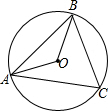 如图,AB是圆形人工湖上的一座桥,桥长100米,在湖岸上一点C,测得∠ACB=60°,则这个人工湖的直径为( )
如图,AB是圆形人工湖上的一座桥,桥长100米,在湖岸上一点C,测得∠ACB=60°,则这个人工湖的直径为( )
 如图,AB是圆形人工湖上的一座桥,桥长100米,在湖岸上一点C,测得∠ACB=60°,则这个人工湖的直径为( )
如图,AB是圆形人工湖上的一座桥,桥长100米,在湖岸上一点C,测得∠ACB=60°,则这个人工湖的直径为( )| A. | 50$\sqrt{3}$ | B. | $\frac{100}{3}$$\sqrt{3}$ | C. | $\frac{200}{3}$$\sqrt{3}$ | D. | 200$\sqrt{3}$ |
5.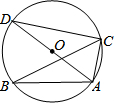 如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=35°,则∠CAD的度数是( )
如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=35°,则∠CAD的度数是( )
 如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=35°,则∠CAD的度数是( )
如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=35°,则∠CAD的度数是( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
 实数a、b在数轴上的位置如图所示,化简:|b-a|-$\sqrt{{b}^{2}}$.
实数a、b在数轴上的位置如图所示,化简:|b-a|-$\sqrt{{b}^{2}}$.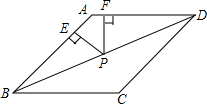 如图,在菱形ABCD中,AB=4,∠A=120°,点P在对角线BD上,PE⊥AB于点E,PF⊥AD于点F,则PE+PF=2$\sqrt{3}$.
如图,在菱形ABCD中,AB=4,∠A=120°,点P在对角线BD上,PE⊥AB于点E,PF⊥AD于点F,则PE+PF=2$\sqrt{3}$.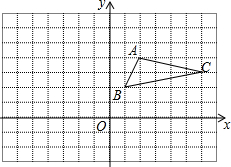 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.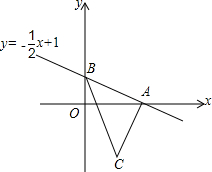 如图,已知直线y=-$\frac{1}{2}$x+1与坐标轴交于A、B两点,C(1,-2),点P在y轴的负半轴上,且S△PAB=S△ABC.
如图,已知直线y=-$\frac{1}{2}$x+1与坐标轴交于A、B两点,C(1,-2),点P在y轴的负半轴上,且S△PAB=S△ABC.