题目内容
20．若一个三角形三个内角度数的比为2：3：7，那么这个三角形是（ ）| A． | 钝角三角形 | B． | 锐角三角形 | C． | 直角三角形 | D． | 等边三角形 |
分析 由于三角形三个内角度数的比为2：3：7，则可设三角形三个内角度数分别为2x，3x，7x，利用三角形内角和定理可列方程2x+3x+7x=180°，解得x=15°，然后分别计算三个角的度数，再根据三角形的分类进行判断．
解答 解：设三角形三个内角度数分别为2x，3x，7x，
根据三角形内角和定理得2x+3x+7x=180°，解得x=15°，
所以2x=30°，3x=45°，7x=105°，
所以这个三角形为钝角三角形．
故选A．
点评 本题考查了三角形内角和定理：三角形内角和是180°．运用方程的思想解决此题比较简便．
练习册系列答案
相关题目
如图，△ABC与△A1B1C1关于直线l对称，且∠A=92°，∠C1=32°，则∠B的度数为56°．
如图所示，AD∥BC，∠A=∠C，求∠AFB+∠CEA的度数．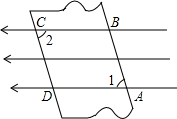
如图，在一束平行光线中插入一张对边平行的纸板，如果光线与纸板右下方所成的∠1是72°15′，那么光线与纸板左上方所成的∠2是多少度？为什么？
9．下列图形中，旋转120°后能与原图形重合的是（ ）
| A． | 等边三角形 | B． | 正方形 | C． | 正五边形 | D． | 正八边形 |
10．-4的倒数是（ ）
| A． | 4 | B． | -$\frac{1}{4}$ | C． | $\frac{1}{4}$ | D． | 16 |