题目内容
3.若点M(-7,m)、N(-8,n)都在函数y=-(k2+2k+4)x+1(k为常数)的图象上,则m和n的大小关系是( )| A. | m>n | B. | m<n | C. | m=n | D. | 不能确定 |
分析 根据一次函数的变化趋势即可判断m与n的大小.
解答 解:∵k2+2k+4=(k+1)2+3>0
∴-(k2+2k+4)<0,
∴该函数是y随着x的增大而减少,
∵-7>-8,
∴m<n,
故选(B)
点评 本题考查一次函数的性质,解题的关键是判断k2+2k+4与0的大小关系,本题属于中等题型.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
18.若正方形的外接圆半径为2,则其内切圆半径为( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
15.已知函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是( )
| A. | 当a=1时,函数图象经过点(-1,1) | |
| B. | 当a=-2时,函数图象与x轴没有交点 | |
| C. | 若a<0,函数图象的顶点始终在x轴的下方 | |
| D. | 若a>0,则当x≥1时,y随x的增大而增大 |
11.下列说法错误的是( )
| A. | 平移和旋转都不改变图形的形状和大小 | |
| B. | 成中心对称的两个图形中,对应点连线的中点是对称中心 | |
| C. | 在平移和旋转图形的过程中,对应角相等,对应线段相等且平行 | |
| D. | 一个图形和它经过旋转后所得的图形中,对应点到旋转中心的距离相等 |
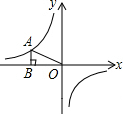 如图,一支反比例函数y=$\frac{k}{x}$的图象经过点A,作AB⊥x轴于点B,连接OA,若S△AOB=3,则k的值为( )
如图,一支反比例函数y=$\frac{k}{x}$的图象经过点A,作AB⊥x轴于点B,连接OA,若S△AOB=3,则k的值为( ) 如图,点P是⊙O外一点,过点P作⊙O的切线PA,切点为A,连接PO,延长PO交⊙O于点B,若∠P=30°,PA=3$\sqrt{3}$,则弧AB的长为2π.
如图,点P是⊙O外一点,过点P作⊙O的切线PA,切点为A,连接PO,延长PO交⊙O于点B,若∠P=30°,PA=3$\sqrt{3}$,则弧AB的长为2π.