题目内容
8.观察下列各式:$\frac{2}{1×3}$=$\frac{1}{1}$-$\frac{1}{3}$;
$\frac{2}{2×4}$=$\frac{1}{2}$-$\frac{1}{4}$;
$\frac{2}{3×5}$=$\frac{1}{3}$-$\frac{1}{5}$;
…
请利用你所得结论,化简代数式:$\frac{1}{1×3}$+$\frac{1}{2×4}$+$\frac{1}{3×5}$+…+$\frac{1}{n(n+2)}$(n≥3且n为整数),其结果为$\frac{3{n}^{2}+5n}{4(n+1)(n+2)}$.
分析 根据所列的等式找到规律$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),由此计算$\frac{1}{1×3}$+$\frac{1}{2×4}$+$\frac{1}{3×5}$+…+$\frac{1}{n(n+2)}$的值.
解答 解:∵$\frac{2}{1×3}$=$\frac{1}{1}$-$\frac{1}{3}$,
$\frac{2}{2×4}$=$\frac{1}{2}$-$\frac{1}{4}$,
$\frac{2}{3×5}$=$\frac{1}{3}$-$\frac{1}{5}$,
…
∴$\frac{2}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
∴$\frac{1}{1×3}$+$\frac{1}{2×4}$+$\frac{1}{3×5}$+…+$\frac{1}{n(n+2)}$=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{n}$-$\frac{1}{n+2}$)=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)=$\frac{3{n}^{2}+5n}{4(n+1)(n+2)}$.
故答案是:$\frac{3{n}^{2}+5n}{4(n+1)(n+2)}$..
点评 此题主要考查了数字变化类,此题在解答时,看出的是左右数据的特点是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图,在边长为2的菱形ABCD中,∠A=60°,DE⊥AB,DF⊥BC,则△DEF的周长为( )
如图,在边长为2的菱形ABCD中,∠A=60°,DE⊥AB,DF⊥BC,则△DEF的周长为( )
 如图,在边长为2的菱形ABCD中,∠A=60°,DE⊥AB,DF⊥BC,则△DEF的周长为( )
如图,在边长为2的菱形ABCD中,∠A=60°,DE⊥AB,DF⊥BC,则△DEF的周长为( )| A. | 3 | B. | $\sqrt{3}$ | C. | 6 | D. | $3\sqrt{3}$ |
19.一组数据:6,4,a,3,2,它的平均数是4,则它的中位数与方差分别是( )
| A. | 4和2 | B. | 4.5和$\sqrt{2}$ | C. | 4和$\sqrt{2}$ | D. | 4.5和2 |
16. 如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( )
如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( )
 如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( )
如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( )| A. | ∠BAO与∠CAO相等 | B. | ∠BAC与∠ABD互补 | C. | ∠BAO与∠ABO互余 | D. | ∠ABO与∠DBO不等 |
3.若点M(-7,m)、N(-8,n)都在函数y=-(k2+2k+4)x+1(k为常数)的图象上,则m和n的大小关系是( )
| A. | m>n | B. | m<n | C. | m=n | D. | 不能确定 |
17.某校举行“激情五月,唱响青春”为主题的演讲比赛,决赛阶段只剩下甲、乙、丙、丁四名同学,则甲、乙同学获得前两名的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
16.已知x-y=-3,xy=2,则(x+2)(y-2)的值是( )
| A. | 4 | B. | -8 | C. | 12 | D. | 0 |
 如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(-4,0)、B(0,3),抛物线y=-x2+2x+1与y轴交于点C.
如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(-4,0)、B(0,3),抛物线y=-x2+2x+1与y轴交于点C.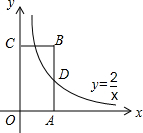 如图,反比例函数y=$\frac{2}{x}$的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为4.
如图,反比例函数y=$\frac{2}{x}$的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为4.