题目内容
5. 如图,△ABC是等边三角形,∠CBD=90°,BD=BC,则∠1的度数是75°.
如图,△ABC是等边三角形,∠CBD=90°,BD=BC,则∠1的度数是75°.
分析 根据等边三角形的性质得出AB=BC,∠ABC=60°,然后证得△ABD是等腰三角形,求得∠BDA=15°,根据等腰直角三角形的性质得出∠BCD=∠BDC=45°,即可得出∠ADC=45°-15°=30°,然后根据三角形外角的性质求得即可.
解答 解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∵BD=BC,
∴AB=BD,
∴∠BAD=∠BDA,
∵∠CBD=90°,
∴∠ABD=90°+60°=150°,
∴∠BDA=15°,
∵∠CBD=90°,BD=BC,
∴∠BCD=∠BDC=45°,
∴∠ADC=45°-15°=30°,
∴∠1=∠ADC+∠BCD=30°+45°=75°.
故答案为75°.
点评 本题考查了等边三角形的性质,等腰直角三角形的性质,等腰三角形的判定和性质,三角形外角的性质,熟练掌握这些性质是解题的关键.

练习册系列答案
相关题目
16. 下列哪个图形经过折叠能围成一个符合条件的正方体( )
下列哪个图形经过折叠能围成一个符合条件的正方体( )
 下列哪个图形经过折叠能围成一个符合条件的正方体( )
下列哪个图形经过折叠能围成一个符合条件的正方体( )| A. |  | B. |  | C. |  | D. |  |
13.下列各组数中,互为相反数的是( )
| A. | |-$\frac{7}{8}$|和-$\frac{7}{8}$ | B. | |-$\frac{7}{8}$|和-$\frac{8}{7}$ | C. | |-$\frac{7}{8}$|和$\frac{7}{8}$ | D. | |-$\frac{7}{8}$|和$\frac{8}{7}$ |
 已知:如图,AB=DE,BC=EF,∠B=∠E,求证:AC∥DF.
已知:如图,AB=DE,BC=EF,∠B=∠E,求证:AC∥DF. 已知:如图,AB=AD,∠D=∠B,∠1=∠2,求证:
已知:如图,AB=AD,∠D=∠B,∠1=∠2,求证: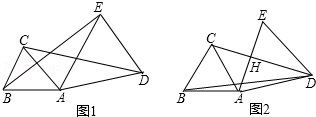
 已知:点D在AB上,点E在AC上,BE⊥AC,CD⊥AB,AB=AC,求证:∠B=∠C.
已知:点D在AB上,点E在AC上,BE⊥AC,CD⊥AB,AB=AC,求证:∠B=∠C.